Homework 5
BSTA 550
Directions
Please turn in this homework on Sakai. Please submit your homework in pdf or html format.
You can type your work on your computer or submit a photo of your written work or any other method that can be turned into a pdf. The Adobe Scan phone app is an easy way to scan photos and compile into a PDF. Please let me know if you greatly prefer to submit a physical copy. We can work out another way for you to turn in homework.
You must show all of your work to receive credit.
Extra problems do not need to be turned in!
Questions
The following table shows the results of a survey in which the subjects were a sample of 300 adults residing in a certain metropolitan area. Each subject was asked to indicate which of three policies they favored with respect to smoking in public places. (Table is from Biostatistics: A Foundation for Analysis in the Health Sciences, 10th Edition, Daniel, Wayne W.; Cross, Chad L., pg. 630)
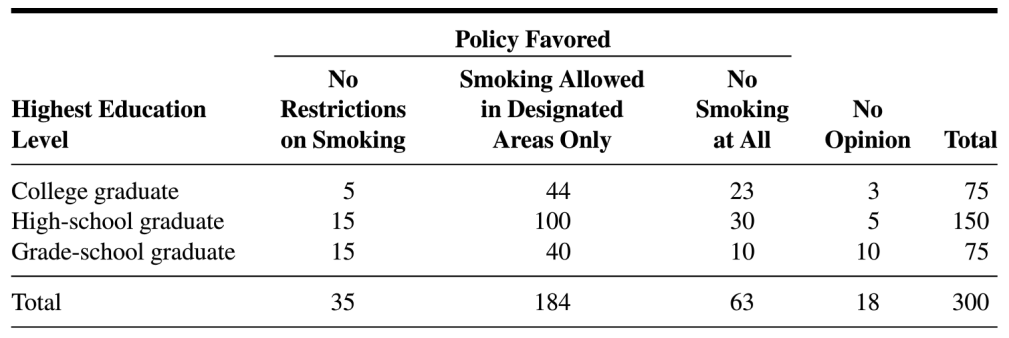
Let \(X=\) highest education level and \(Y=\) policy favored. We can let \(X=1\) for college graduate, \(X=2\) for high-school graduate, etc., and similarly for \(Y\), or just keep the category names for the different levels of \(X\) and \(Y\)
Make a table for the joint pmf \(p_{X,Y}(x,y)\) and briefly describe in words what the values are the probability of.
Find the marginal pmf \(p_{X}(x)\) and briefly describe in words what the values are the probability of.
Find the marginal pmf \(p_{Y}(y)\) and briefly describe in words what the values are the probability of.
Make a table for the joint cdf \(F_{X,Y}(x,y)\) and briefly describe in words what the values are the probability of.
Find the marginal cdf \(F_{X}(x)\) and briefly describe in words what the values are the probability of.
Find the marginal cdf \(F_{Y}(y)\) and briefly describe in words what the values are the probability of.
Let \(X_1, X_2, \ldots, X_n\) be i.i.d. random variables with common pdf \(f_X(x)\) and cdf \(F_X(x)\). Find the pdf for the random variable \(Z\), where \(Z = \max(X_1, X_2, \ldots, X_n)\).
Let \(X\) and \(Y\) be independent random variables with respective pdf’s \(f_X(x)=\frac{1}{5}\), for \(0\leq x\leq 5\), and \(f_Y(y)=2e^{-2y}\), for \(y>0\).
- Find the joint distribution \(f_{X,Y}(x,y)\).
- Find the probability that \(X\) is less than \(Y\).
- Let \(Z\) be the random variable that is the smaller of \(X\) and \(Y\). Find the cumulative distribution function for \(Z\).
- Find the pdf for Z.
Suppose that the random variables \(X\) and \(Y\) have joint density \(f_{X,Y}(x,y)\), for \(0<x<1\), and \(\frac{1}{2}<y<1\). Set up the equation for the cdf of \(Z\), where \(Z=X/Y\).
Hint: First determine what the possible values for \(Z\) are. Then make a sketch of the domain of the joint pdf and shade in the region representing the cdf of Z for different values of \(z\). Make sure to pay close attention to how the region we need to integrate over changes as \(z\) changes. The cdf has two different cases depending on the value of \(z\). Plug in specific values of \(z\) and shade in the region representing the cdf to see why two different cases are needed.
Extra problems
- Freddy and Jane have entered a game in which they each win between 0 and 2 dollars. If X is the amount Freddy wins, and Y is the amount that Jane wins, they believe that the joint density of their winnings will be \[f_{X,Y}(x, y) = \dfrac{1}{4}xy \text{ for } 0 \leq x \leq 2 \text{ and } 0 \leq y \leq 2\] and \(f_{X,Y}(x, y) = 0\) otherwise. Find the probability that their combined winnings exceed 2, i.e., find \(P(X + Y > 2)\).