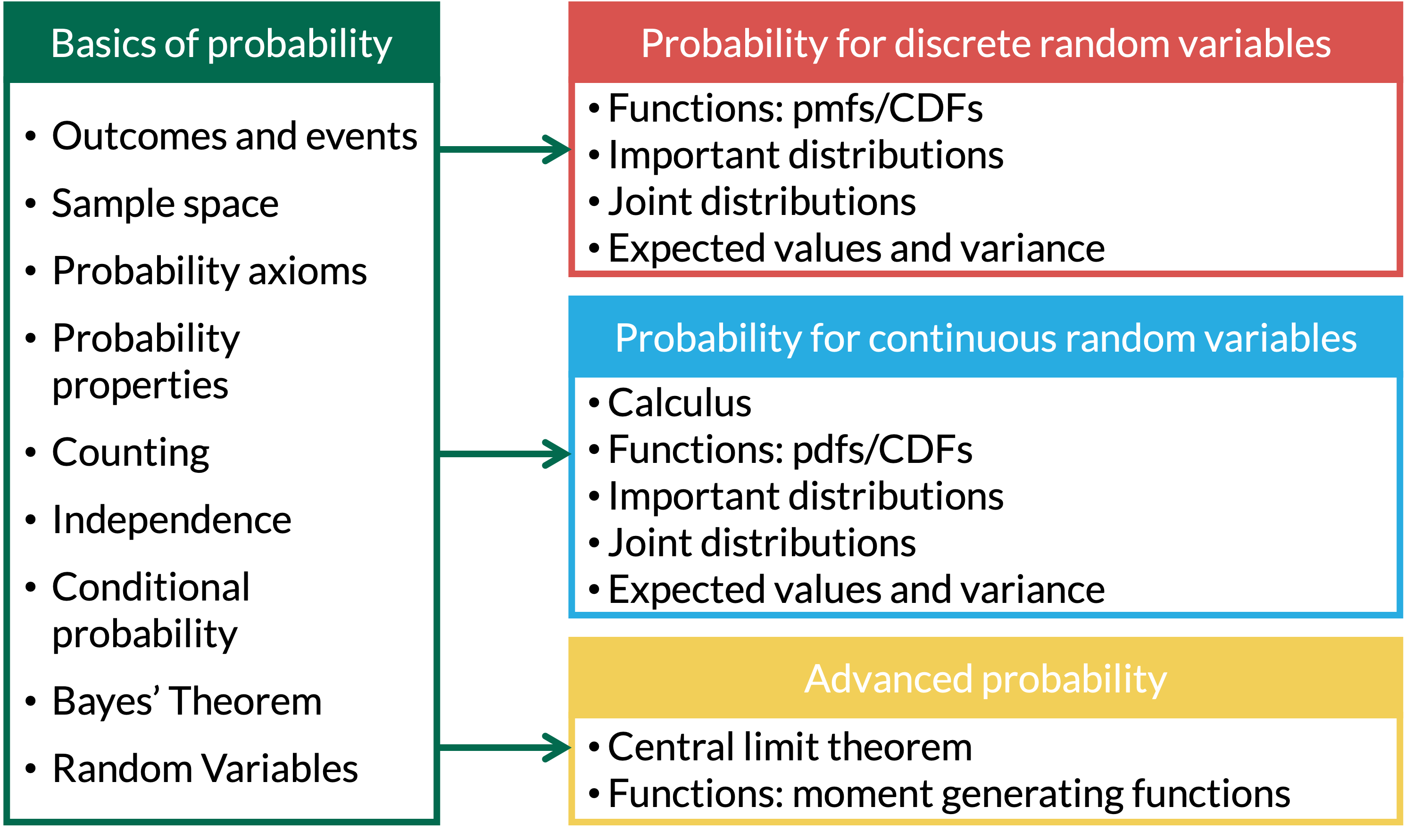
set.seed(1002)
reps = 10000
rolls = replicate(reps, sample(x = 1:6, size = 2, replace = TRUE))
rolls[, 1:10] [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 4 5 5 5 6 5 2 4 3 4
[2,] 1 4 6 3 1 1 5 5 6 3 [1] FALSE FALSE FALSE FALSE TRUE FALSE TRUE FALSE FALSE TRUE [1] FALSE FALSE FALSE FALSE TRUE FALSE FALSE FALSE FALSE FALSE