Lesson 9: Cumulative distribution functions (CDFs)

Nicky Wakim

2025-10-22

Learning Objectives

Understand the definition of cumulative distribution functions (CDFs) for discrete and continuous random variables.
Compute CDFs for given probability mass functions (pmfs).
Compute CDFs for given probability density functions (pdfs) and pdfs from CDFs.

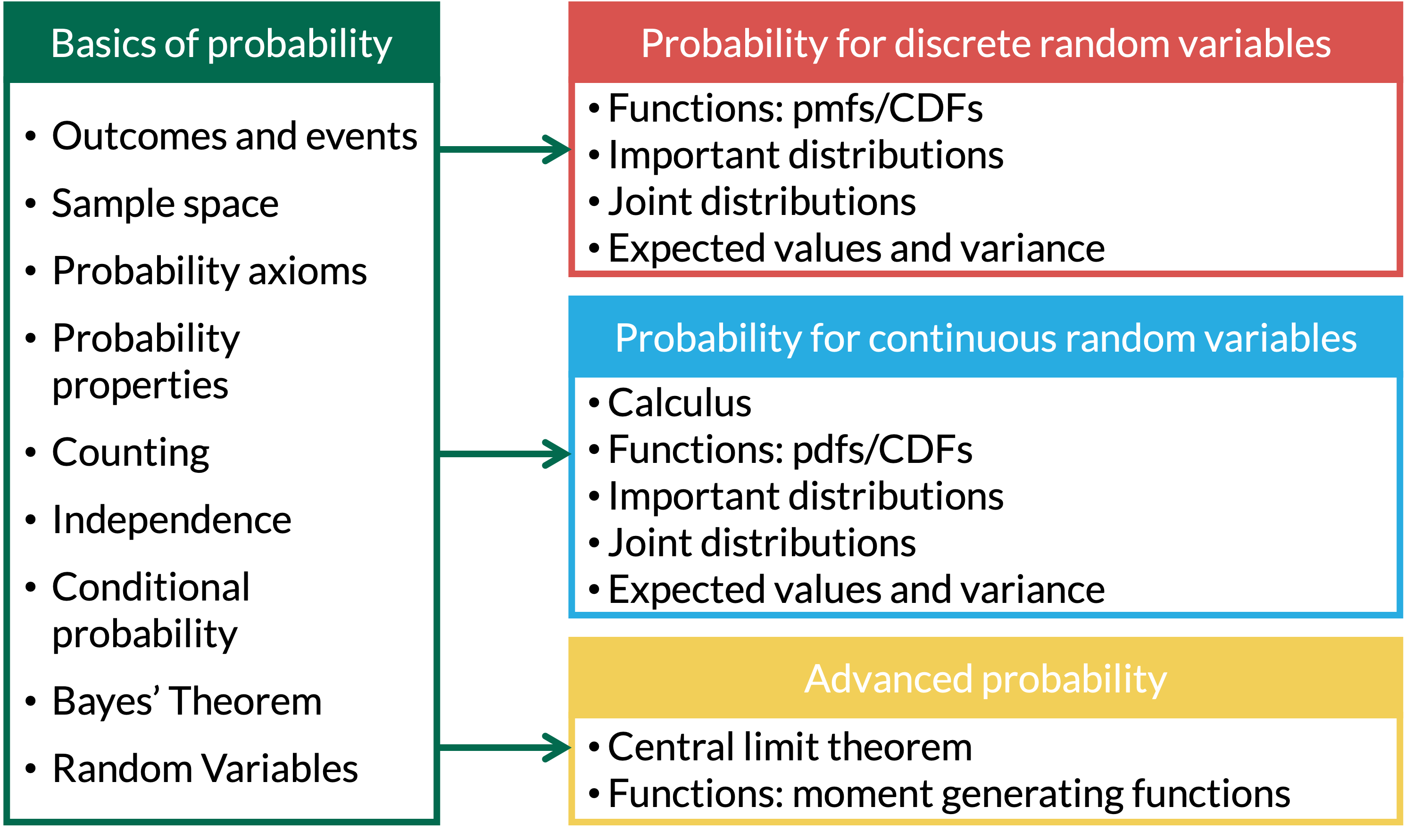
Where are we?

Learning Objectives

Understand the definition of cumulative distribution functions (CDFs) for discrete and continuous random variables.

Compute CDFs for given probability mass functions (pmfs).
Compute CDFs for given probability density functions (pdfs) and pdfs from CDFs.

What is a cumulative distribution function?

Cumulative distribution function (CDF) for discrete random variable

The cumulative distribution function (cdf) of a discrete RV \(X\) with pmf \(p_X(x)\), is defined for every value \(x\) by \[F_X(x) = \mathbb{P}(X \leq x) = \sum \limits_{\{all\ y:\ y\leq x\}}p_X(y)\]

\(F(x)\) is increasing or flat (never decreasing)
\(\min\limits_x F(x) = 0\)
\(\max\limits_xF(x)=1\)
CDF is a step function

Cumulative distribution function (CDF) for continuous random variable

The cumulative distribution function (cdf) of a continuous RV \(X\), is the function \(F_X(x)\), such that for all real values of \(x\), \[F_X(x)= \mathbb{P}(X \leq x) = \int_{-\infty}^x f_X(s)ds\]

Remarks: In general, \(F_X(x)\) is increasing and

\(\lim_{x\rightarrow -\infty} F_X(x)= 0\)
\(\lim_{x\rightarrow \infty} F_X(x)= 1\)
\(P(X > a) = 1 - P(X \leq a) = 1 - F_X(a)\)
\(P(a \leq X \leq b) = F_X(b) - F_X(a)\)

How to define CDFs for discrete and continuous RVs?

Discrete RV \(X\):

pmf: \(p_X(x) = P(X=x)\)
CDF: \(F_X(x) = P(X \leq x) = \sum\limits_{\{all\ y:\ y\leq x\}} p_X(y)\)

Continuous RV \(X\):

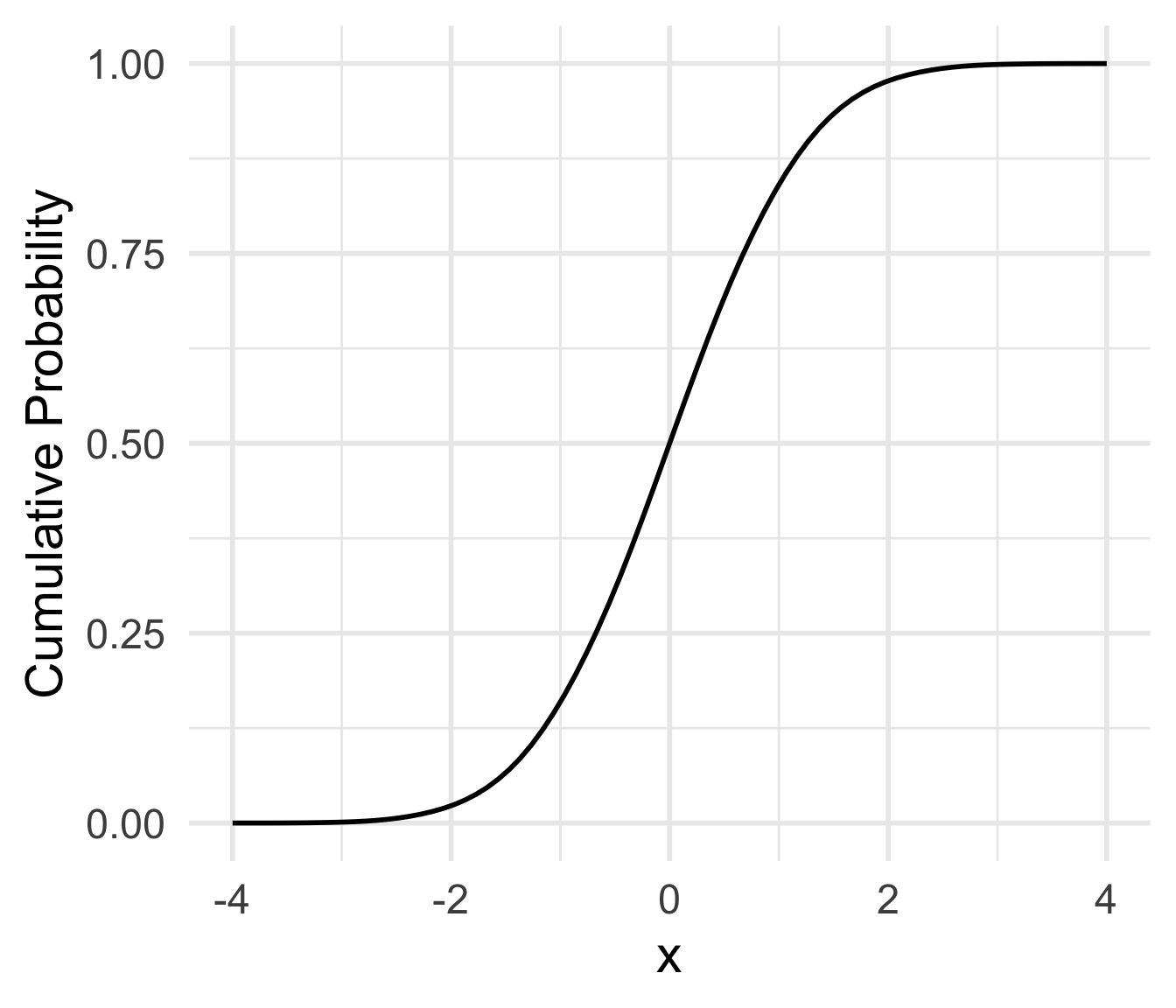
density: \(f_X(x)\)
probability: \(P(a \leq X \leq b) = \int_a^b f_X(x)dx\)
CDF: \(F_X(x) = P(X \leq x) = \int_{-\infty}^x f_X(s)ds\)

Learning Objective

Understand the definition of cumulative distribution functions (CDFs) for discrete and continuous random variables.

Compute CDFs for given probability mass functions (pmfs).

Compute CDFs for given probability density functions (pdfs) and pdfs from CDFs.

Falls in Older Adults Revisited (1/5)

Example 1: Falls in Older Adults

A major public health concern is falls among older adults (age 65+). National data suggests that 25% of older adults will experience at least one fall within a given year. A community health program is tracking a random group of \(n = 8\) older adults for one year. Assume the likelihood of falling is independent from person to person.

Let \(X\) be the random variable representing the number of individuals in this group who experience at least one fall.

Write the CDF of \(X\) and make a table of values.
Use R to calculate the cumulative probability for each possible value of \(X\).
Plot the CDF of \(X\).
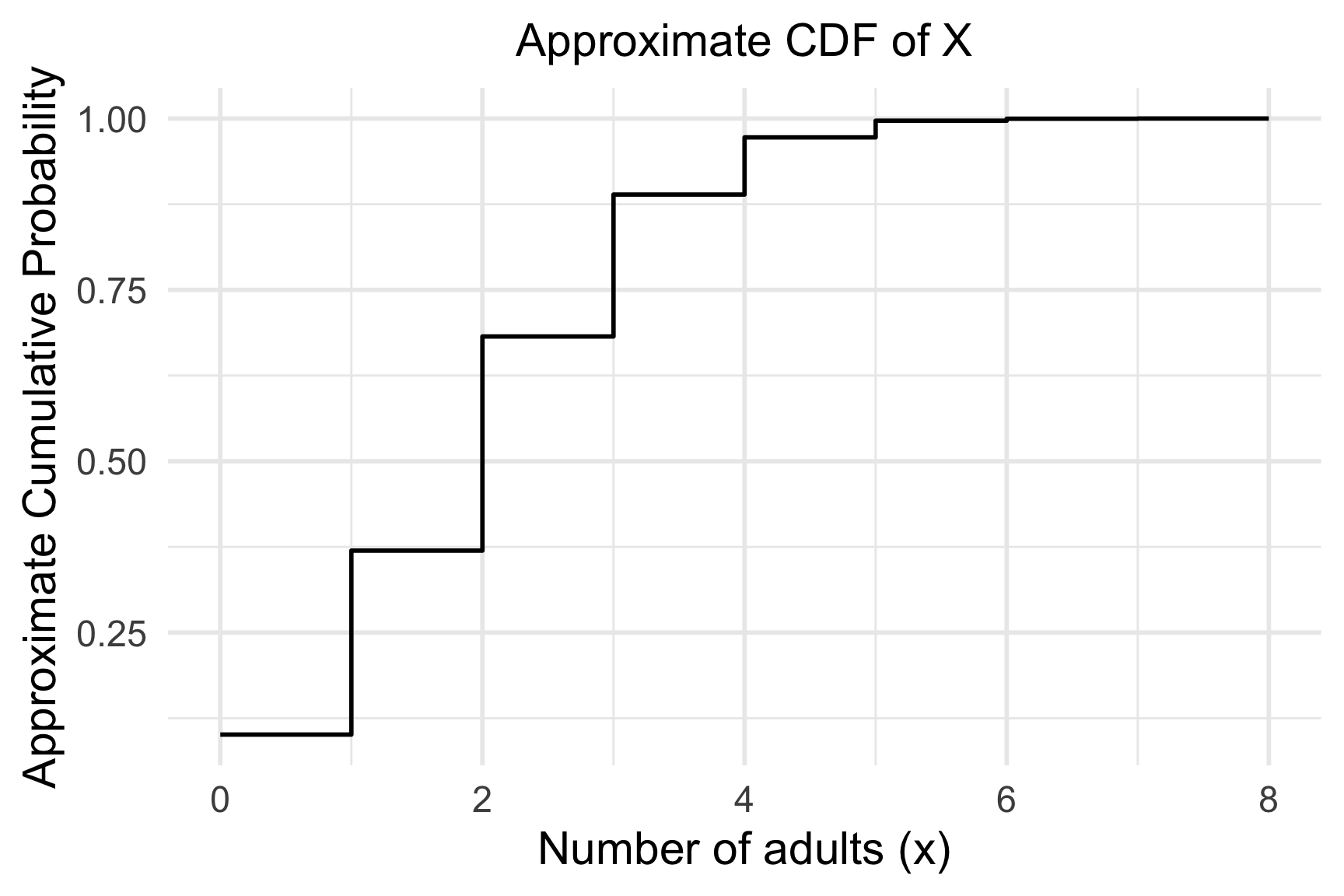
Simulate \(X\) for 10000 groups and plot the approximated CDF.

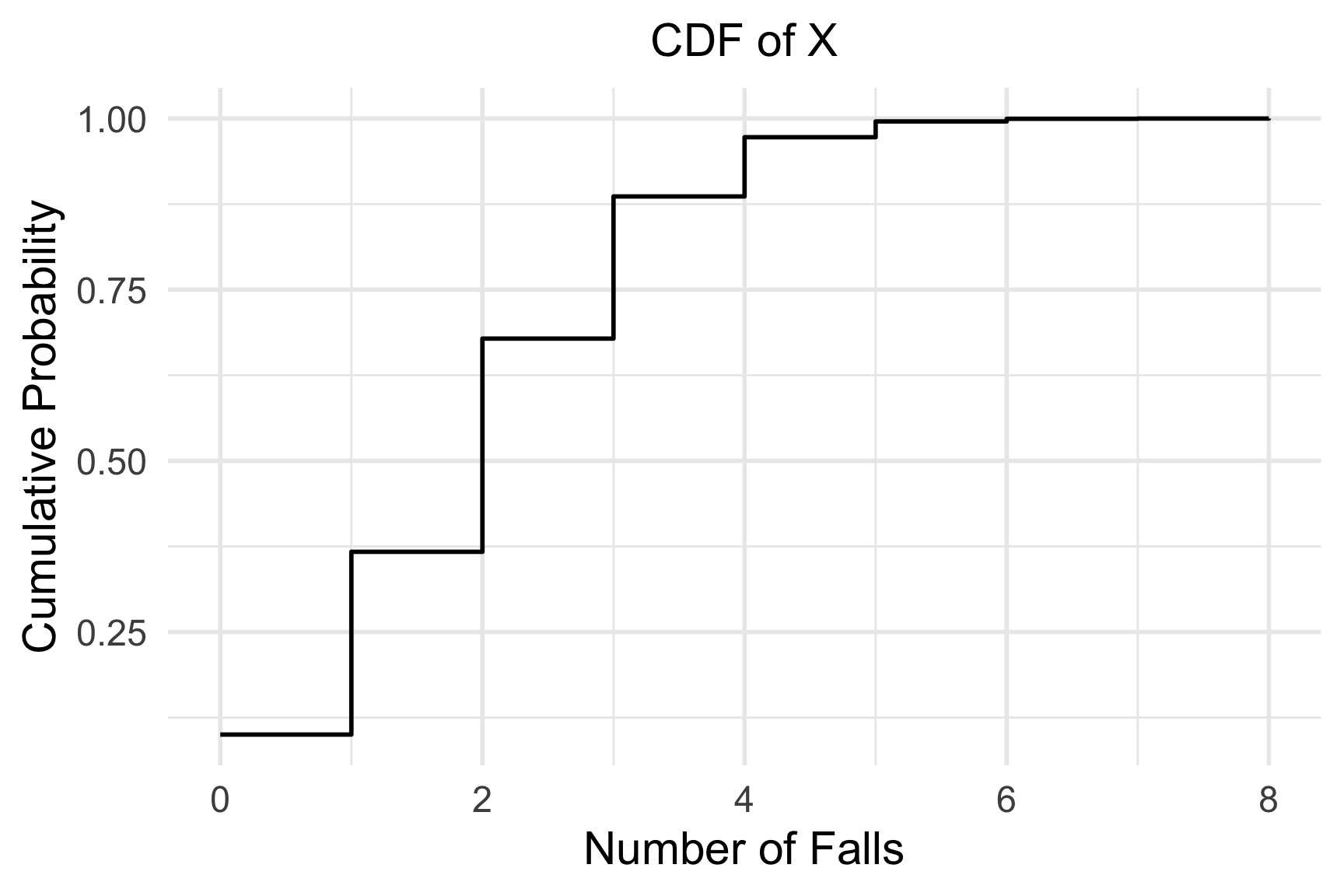
Recall our pmf: \[P(X = x) = \binom{8}{x} 0.25^x 0.75^{8-x}, x= 0, 1, 2, \dots, 8 \]

Falls in Older Adults Revisited (2/5)

Example 1: Falls in Older Adults

Write the CDF of \(X\).

Recall our pmf: \[P(X = x) = \binom{8}{x} 0.25^x 0.75^{8-x}, x= 0, 1, 2, \dots, 8 \]

\[F_X(x) = P(X \leq x) = \sum \limits_{k=0}^{x} \binom{8}{k} 0.25^y 0.75^{8-k}\]

Falls in Older Adults Revisited (3/5)

Example 1: Falls in Older Adults

Use R to calculate the cumulative probability for each possible value of \(X\).

n = 8
p = 0.25

falls_cdf <- tibble(
  x = 0:n,
  c_prob = pbinom(x, size = n, prob = p)
)

falls_cdf

# A tibble: 9 × 2
      x c_prob
  <int>  <dbl>
1     0  0.100
2     1  0.367
3     2  0.679
4     3  0.886
5     4  0.973
6     5  0.996
7     6  1.00 
8     7  1.00 
9     8  1

Falls in Older Adults Revisited (4/5)

Example 1: Falls in Older Adults

Plot the CDF of \(X\).

ggplot(
  falls_cdf,
  aes(x = x, y = c_prob)
       ) +
  geom_step(
    size = 1, 
    color = "black"
    ) +
  labs(
    x = "Number of Falls",
    y = "Cumulative Probability",
    title = "CDF of X"
    )

Falls in Older Adults Revisited (4/5)

Example 1: Falls in Older Adults

Simulate \(X\) for 10000 groups and plot the approximated CDF.

set.seed(4764)
reps = 10000

sims = rbinom(n = reps, 
              size = n, 
              prob = p)

sims %>% head(., 14)

 [1] 2 1 2 1 3 3 2 2 4 2 3 0 2 0

falls2 <- tibble(x = 0:n) %>%
  rowwise() %>%
  mutate(c_prob = sum(sims <= x) / reps)

ggplot(falls2, aes(x = x, y = c_prob)) +
  geom_step(size = 1, color = "black") +
  labs(
    title = "Approximate CDF of X",
    x = "Number of adults (x)",
    y = "Approximate Cumulative Probability"
  )

Learning Objective

Understand the definition of cumulative distribution functions (CDFs) for discrete and continuous random variables.
Compute CDFs for given probability mass functions (pmfs).

Compute CDFs for given probability density functions (pdfs) and pdfs from CDFs.

Let’s demonstrate the CDF with an example

Example 2

Let \(f_X(x)= 2\), for \(2.5 \leq x \leq 3\). Find \(F_X(x)\).

Derivatives of the CDF

Theorem 1

If \(X\) is a continuous random variable with pdf \(f_X(x)\) and cdf \(F_X(x)\), then for all real values of \(x\) at which \(F'_X(x)\) exists, \[\frac{d}{dx} F_X(x)= F'_X(x) = f_X(x)\]

Finding the PDF from a CDF

Example 3

Let \(X\) be a RV with cdf \[F_X(x)= \left\{ \begin{array}{ll} 0 & \quad x < 2.5 \\ 2x-5 & \quad 2.5 \leq x \leq 3 \\ 1 & \quad x > 3 \end{array} \right.\] Find the pdf \(f_X(x)\).