
Chapter 24: Continuous RVs and PDFs
2024-11-06
Learning Objectives
Distinguish between discrete and continuous random variables.
Calculate probabilities for continuous random variables.
Calculate and graph a density (i.e., probability density function, PDF).
Calculate and graph a CDF (i.e., a cumulative distribution function)
Discrete vs. Continuous RVs
For a discrete RV, the set of possible values is either finite or can be put into a countably infinite list.
Continuous RVs take on values from continuous intervals, or unions of continuous intervals
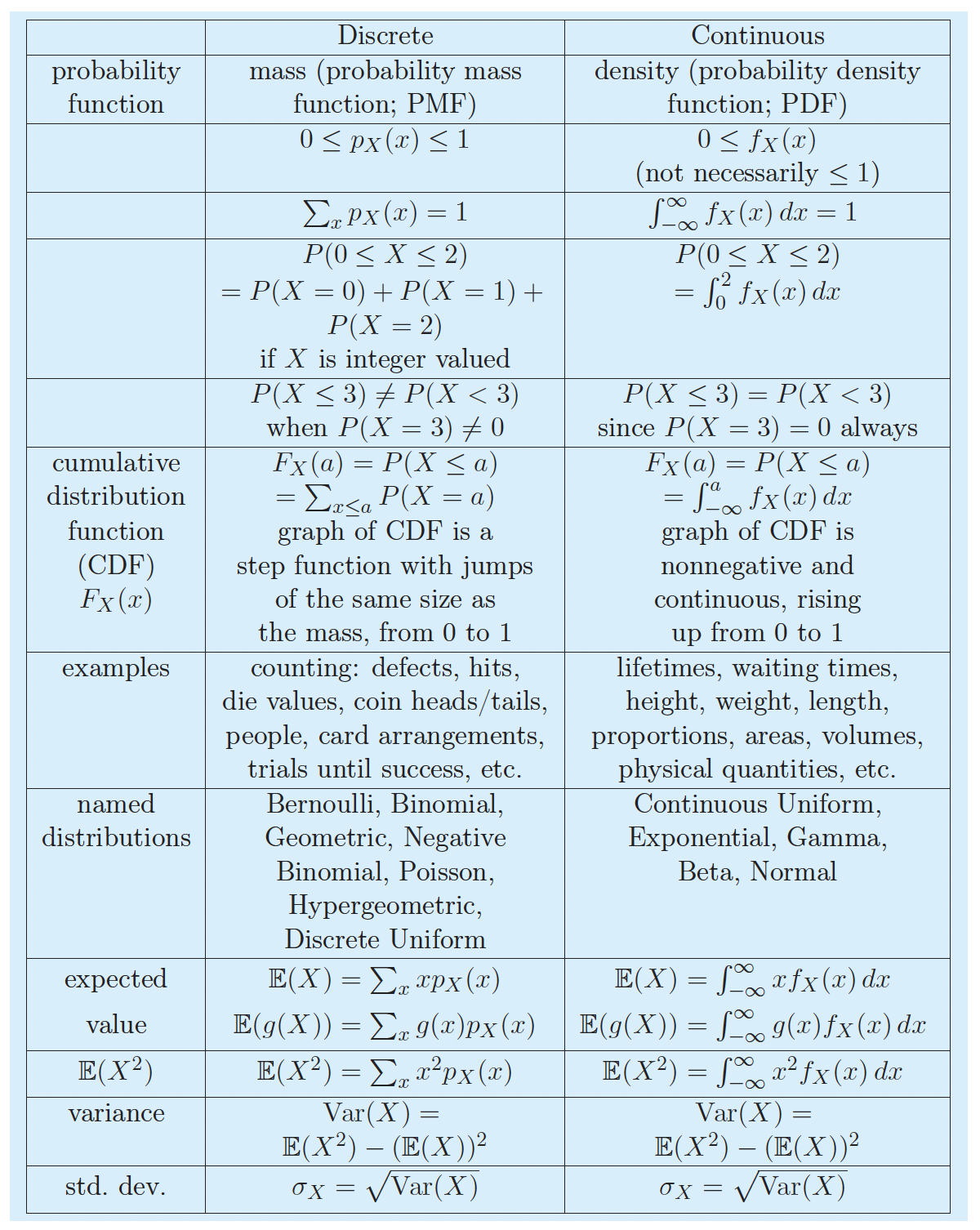
How to define probabilities for continuous RVs?
Discrete RV \(X\):
- pmf: \(p_X(x) = P(X=x)\)
Continuous RV \(X\):

- density: \(f_X(x)\)
- probability: \(P(a \leq X \leq b) = \int_a^b f_X(x)dx\)
What is a probability density function?
Probability density function
The probability distribution, or probability density function (pdf), of a continuous random variable \(X\) is a function \(f_X(x)\), such that for all real values \(a,b\) with \(a \leq b\),
\[\mathbb{P}(a \leq X \leq b) = \int_a^b f_X(x)dx\]
Remarks:
Note that \(f_X(x) \neq \mathbb{P}(X=x)\)!!!
In order for \(f_X(x)\) to be a pdf, it needs to satisfy the properties
\(f_X(x) \geq 0\) for all \(x\)
\(\int_{-\infty}^{\infty} f_X(x)dx=1\)
Let’s demonstrate the PDF with an example (1/5)
Example 1.1
Let \(f_X(x)= 2\), for \(a \leq x \leq 3\).
- Find the value of \(a\) so that \(f_X(x)\) is a pdf.
Let’s demonstrate the PDF with an example (2/5)
Example 1.2
Let \(f_X(x)= 2\), for \(a \leq x \leq 3\).
- Find \(\mathbb{P}(2.7 \leq X \leq 2.9)\).
Let’s demonstrate the PDF with an example (3/5)
Example 1.3
Let \(f_X(x)= 2\), for \(a \leq x \leq 3\).
- Find \(\mathbb{P}(2.7 < X \leq 2.9)\).
Let’s demonstrate the PDF with an example (4/5)
Example 1.4
Let \(f_X(x)= 2\), for \(a \leq x \leq 3\).
- Find \(\mathbb{P}(X = 2.9)\).
Let’s demonstrate the PDF with an example (5/5)
Example 1.5
Let \(f_X(x)= 2\), for \(a \leq x \leq 3\).
- Find \(\mathbb{P}(X \leq 2.8)\).
Chapter 24 Slides