Lesson 10: Transformations
2025-10-27
Learning Objectives
- Find the pdf of a linear rescaling of a random variable
- Find the pdf of a nonlinear transformation of a random variable using the CDF method
Distributions of transformations of random variables
- Often make transformations of RVs
- A function of a random variable is a random variable
- If \(X\) is a random variable and \(g\) is a function then \(Y=g(X)\) is a random variable
- Since \(g(X)\) is a random variable it has a distribution
- Distribution of \(g(X)\) will have a different shape than the distribution of \(X\)
- Two types:
- Linear rescalings: \(g(u) = a + bu\)
- Nonlinear transformations: e.g. \(g(u) = u^2\), \(g(u) = \log(u)\)
Learning Objectives
- Find the pdf of a linear rescaling of a random variable
- Find the pdf of a nonlinear transformation of a random variable using the CDF method
Linear rescaling
Definition: Linear Rescaling
A linear rescaling is a transformation of the form \(g(u) = a + bu\), where \(a\) and \(b\) are constants
Thus, if we have a random variable, \(X\), then a linear rescaling of \(X\) could be \(M = g(X) = a + bX\)
For example, converting temperature from Celsius to Fahrenheit using \(g(u) = 32 + 1.8u\) is a linear rescaling.
Example of linear rescaling (1/4)
Example 1: Linear rescaling of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=1-U\)
- What are the possible values of \(V\)?
- Is \(V\) the same random variable as \(U\)?
- Find \(P(V \le -0.5)\).
- Find the pdf of \(V\).
- Does \(V\) have the same distribution as \(U\)?
Example of linear rescaling (2/4)
Example 1: Linear rescaling of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=1-U\)
- What are the possible values of \(V\)?
- Is \(V\) the same random variable as \(U\)?
Example of linear rescaling (3/4)
Example 1: Linear rescaling of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=1-U\)
- Find \(P(V \le -0.5)\).
Example of linear rescaling (4/4)
Example 1: Linear rescaling of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=1-U\)
- Find the pdf of \(V\).
- Does \(V\) have the same distribution as \(U\)?
Summary of linear rescaling
A linear rescaling of a random variable does not change the basic shape of its distribution, just the range of possible values.
- It can flip it, widen it, condense it, and/or shift it
Remember, do NOT confuse a random variable with its distribution
- The random variable is the numerical quantity being measured
- The distribution is the long run pattern of variation of many observed values of the random variable
Learning Objectives
- Find the pdf of a linear rescaling of a random variable
- Find the pdf of a nonlinear transformation of a random variable using the CDF method
Nonlinear transformations
What happens when we make a nonlinear transformation, like a logarithmic or square root transformation?
Nonlinear transformations do not necessarily preserve the distribution shape
Examples of nonlinear transformations:
- \(g(u) = u^2\)
- \(g(u) = \sqrt{u}\)
- \(g(u) = \log(u)\)
- \(g(u) = e^u\)
- \(g(u) = \dfrac{1}{u}\)
Finding the pdf of a transformation
Let \(M\) be a transformation of \(X\): \(M = g(X)\)
When we have a transformation of \(X\), \(M\), we need to follow the CDF method to find the pdf of \(M\)
We follow CDF method:
Start with the pdf for \(X\)
- aka \(f_{X}(x)\)
Translate the domain of \(X\) to \(M\): find the possible values of \(M\)
Find the CDF of \(M\)
- aka \(F_M(m) = P(M \leq m) = P(g(X) \leq m)\)
- Will require manipulating \(g(X) \leq m\) in terms of \(X\) (aka \(X\) alone on the left side)
Take the derivative of the CDF of \(M\) with respect to \(m\) to find the pdf of \(M\)
- aka \(f_M(m) = \dfrac{d}{dm}F_M(m)\)
Example of nonlinear transformation (1/4)
Example 2: Nonlinear transformation of \(U\)
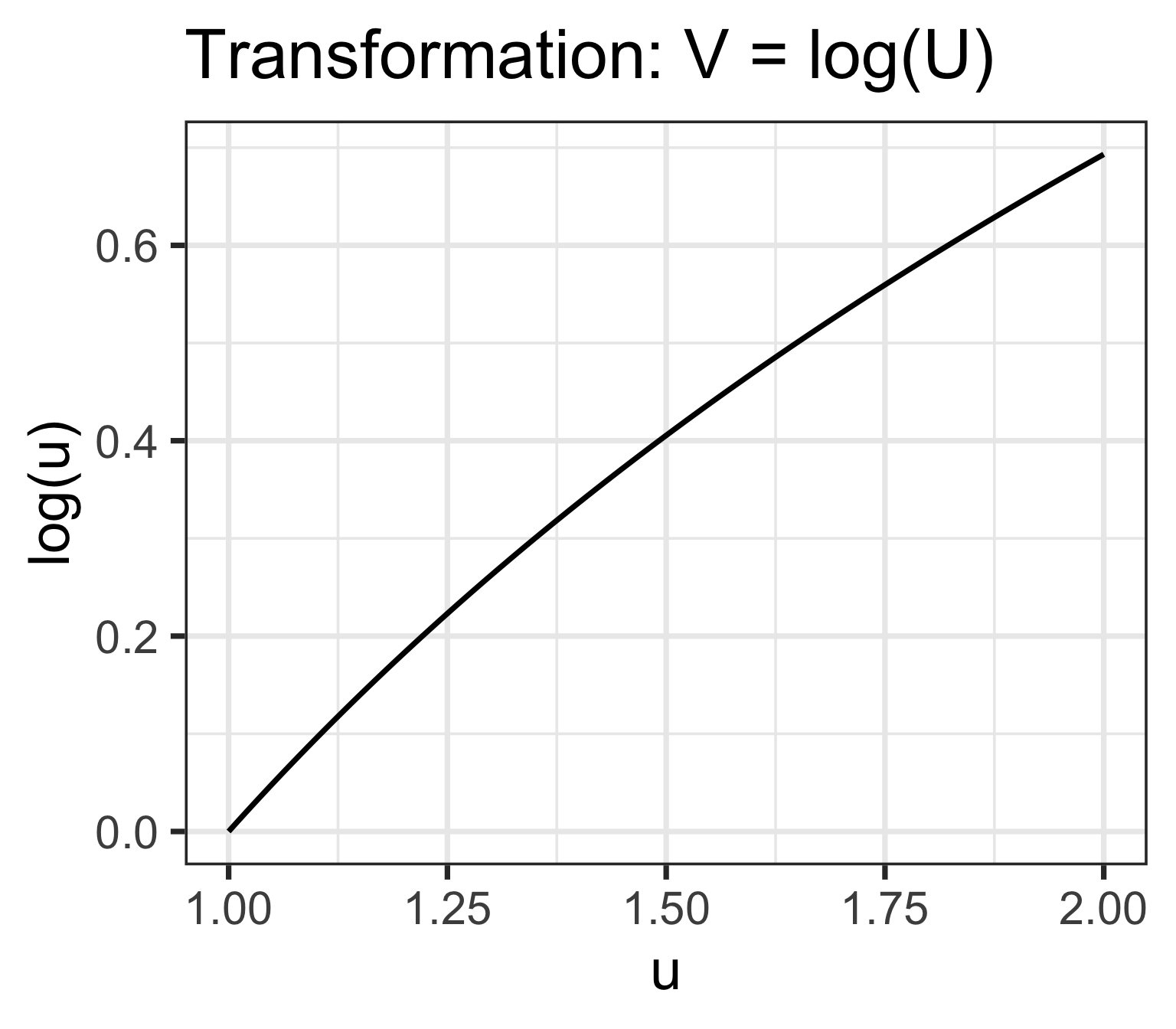
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=\log(U)\)
- What are the possible values of \(V\)?
- Find the CDF of \(V\)
- Find the pdf of \(V\)
Example of nonlinear transformation (2/4)
Example 2: Nonlinear transformation of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=\log(U)\)
- What are the possible values of \(V\)?
Example of nonlinear transformation (3/4)
Example 2: Nonlinear transformation of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=\log(U)\)
- Find the CDF of \(V\)
Example of nonlinear transformation (4/4)
Example 2: Nonlinear transformation of \(U\)
Let \(U\) be a random variable with \(f_U(u)= \dfrac{4}{15}u^3\) for \(1\leq u \leq 2\). Define \(V=\log(U)\)
- Find the pdf of \(V\)
Example of nonlinear transformation: domain (1/4)
Example 3: Nonlinear transformation of \(X\)
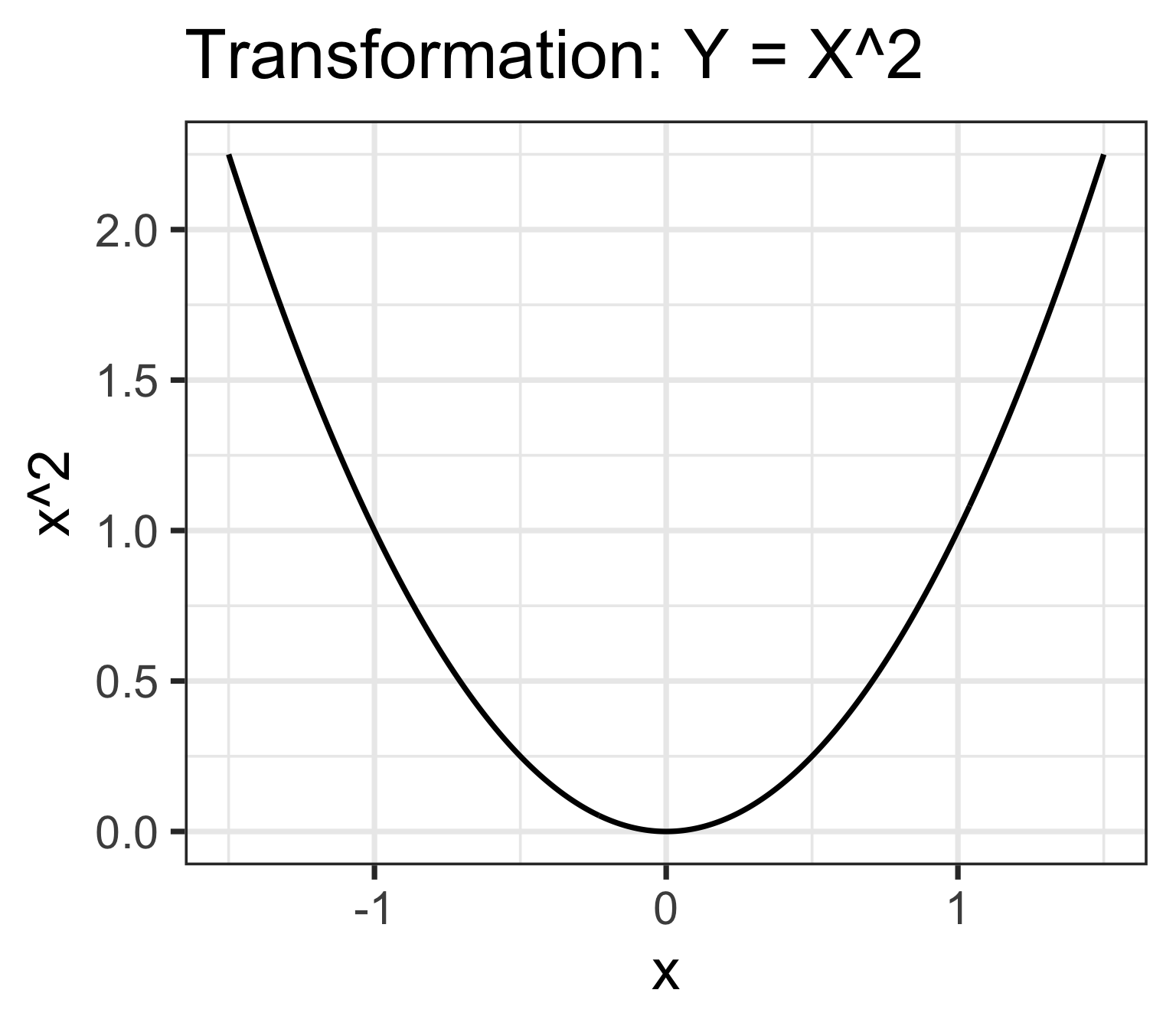
Let \(X\) be a random variable with \(f_X(x)= \dfrac{1}{2}\) for \(-1\leq x \leq 1\). Define \(Y=X^2\)
- What are the possible values of \(Y\)?
- Find the CDF of \(Y\)
- Find the pdf of \(Y\)
Example of nonlinear transformation: domain (2/4)
Example 3: Nonlinear transformation of \(X\)
Let \(X\) be a random variable with \(f_X(x)= \dfrac{1}{2}\) for \(-1\leq x \leq 1\). Define \(Y=X^2\)
- What are the possible values of \(Y\)?
Example of nonlinear transformation: domain (3/4)
Example 3: Nonlinear transformation of \(X\)
Let \(X\) be a random variable with \(f_X(x)= \dfrac{1}{2}\) for \(-1\leq x \leq 1\). Define \(Y=X^2\)
- Find the CDF of \(Y\)
Example of nonlinear transformation: domain (4/4)
Example 3: Nonlinear transformation of \(X\)
Let \(X\) be a random variable with \(f_X(x)= \dfrac{1}{2}\) for \(-1\leq x \leq 1\). Define \(Y=X^2\)
- Find the pdf of \(Y\)
Summary of nonlinear transformations
- Nonlinear transformations can change the shape of a distribution
- Always use the CDF method to find the pdf of a nonlinear transformation of a random variable
- Remember to carefully determine the possible values of the transformed random variable
Lesson 10 Slides