Lesson 11: Joint distributions
2025-10-29
Learning Objectives
Define joint and marginal distributions for discrete and continuous random variables
Calculate or find joint and marginal probabilities, pmf’s, and CDF’s for discrete random variables
Calculate or find joint and marginal probabilities, pdf’s, and CDF’s for continuous random variables
Extra practice on your own: solve double integrals in a mini lesson
Where are we?
Learning Objectives
- Define joint and marginal distributions for discrete and continuous random variables
Calculate or find joint and marginal probabilities, pmf’s, and CDF’s for discrete random variables
Calculate or find joint and marginal probabilities, pdf’s, and CDF’s for continuous random variables
Extra practice on your own: solve double integrals in a mini lesson
What is a joint distribution?
Definition: joint pmf
The joint pmf of a pair of discrete RV’s \(X\) and \(Y\) is \[\begin{aligned} p_{X,Y}(x,y) = & \mathbb{P}(X=x \cap Y=y) \\ = & \mathbb{P}(X=x, Y=y) \end{aligned}\]
Definition: joint pdf
The joint pdf for two continuous RVs (\(X\) and \(Y\)) is \(f_{X,Y}(x,y)\), such that we have the following joint probability: \[\begin{aligned} \mathbb{P}(a \leq X \leq b, & c \leq Y \leq d) = \\ & \int_a^b \int_c^d f_{X,Y}(x,y)dydx \end{aligned}\]
Important properties of joint distributions
Properties of joint pmf’s
A joint pmf \(p_{X,Y}(x,y)\) must satisfy the following properties:
- \(0 \geq p_{X,Y}(x,y) \leq 1\) for all \(x, y\)
- \(\sum \limits_{\{all\ x\}} \sum \limits_{\{all\ y\}} p_{X,Y}(x,y)=1\)
Properties of joint pdf’s
A joint pdf \(f_{X,Y}(x,y)\) must satisfy the following properties:
- \(f_{X,Y}(x,y)\geq 0\) for all \(x,y\)
- \(\displaystyle\int_{-\infty}^{\infty}\displaystyle\int_{-\infty}^{\infty} f_{X,Y}(x,y)dxdy=1\)
- Remember that \(f_{X,Y}(x,y)\neq \mathbb{P}(X=x, Y=y)\)!!!
Marginal distributions
Marginal pmf’s
Suppose \(X\) and \(Y\) are discrete RV’s, with joint pmf \(p_{X,Y}(x,y)\). Then the marginal probability mass functions are
\[p_X(x) = \sum \limits_{\{all\ y\}} p_{X,Y}(x,y)\]
\[p_Y(y) = \sum \limits_{\{all\ x\}} p_{X,Y}(x,y)\]
Marginal pdf’s
Suppose \(X\) and \(Y\) are continuous RV’s, with joint pdf \(f_{X,Y}(x,y)\). Then the marginal probability density functions are \[\begin{aligned} f_X(x)&=& \int_{-\infty}^{\infty} f_{X,Y}(x,y)dy\\ f_Y(y)&=& \int_{-\infty}^{\infty} f_{X,Y}(x,y)dx \end{aligned}\]
Joint cumulative distribution functions (CDFs)
Joint CDF for discrete RVs
The joint CDF of a pair of discrete RV’s \(X\) and \(Y\) is \[\begin{aligned} F_{X,Y}(x,y) = &\mathbb{P}(X \leq x\ and\ Y \leq y) \\ = &\mathbb{P}(X \leq x, Y \leq y) \end{aligned}\]
Joint CDF for continuous RVs
The joint CDF of continuous random variables \(X\) and \(Y\), is the function \(F_{X,Y}(x,y)\), such that for all real values of \(x\) and \(y\), \[\begin{aligned} F_{X,Y}(x,y)= \mathbb{P}(X \leq x, & Y \leq y) = \\ & \int_{-\infty}^x\int_{-\infty}^y f_{X,Y}(s,t)dtds \end{aligned}\]
Learning Objectives
- Define joint and marginal distributions for discrete and continuous random variables
- Calculate or find joint and marginal probabilities, pmf’s, and CDF’s for discrete random variables
Calculate or find joint and marginal probabilities, pdf’s, and CDF’s for continuous random variables
Extra practice on your own: solve double integrals in a mini lesson
Joint distribution for two discrete random variables (1/5)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
Find \(p_{X,Y}(x,y)\)
Find \(\mathbb{P}(X+Y=3)\)
Find \(\mathbb{P}(Y = 1)\)
Find \(\mathbb{P}(Y \leq 2)\)
Find the joint CDF \(F_{X,Y}(x,y)\) for the joint pmf \(p_{X,Y}(x,y)\)
Find the marginal CDFs \(F_{X}(x)\) and \(F_{Y}(y)\)
Joint distribution for two discrete random variables (2/5)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
Find \(p_{X,Y}(x,y)\)
Find \(\mathbb{P}(X+Y=3)\)
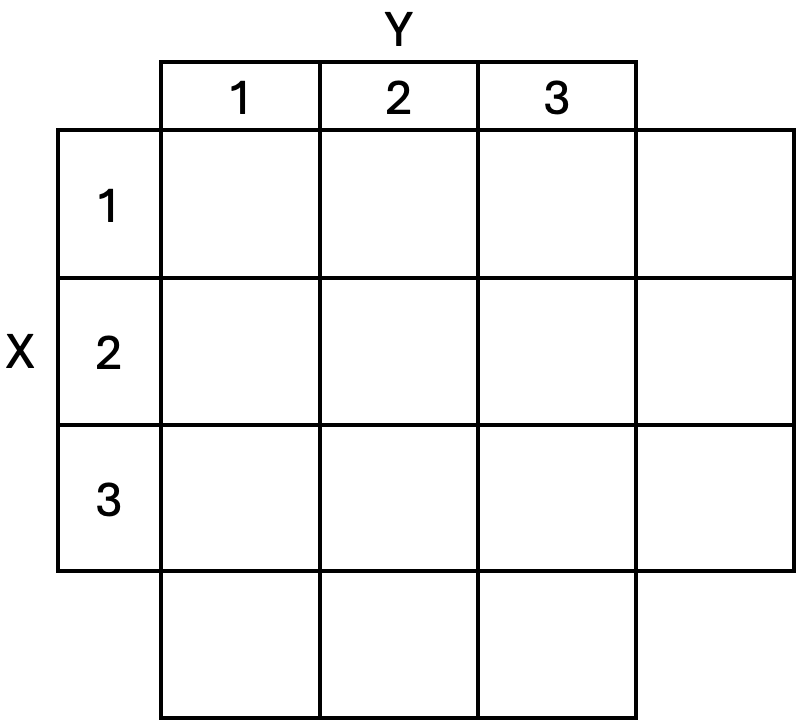
Joint distribution for two discrete random variables (3/5)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
Find \(\mathbb{P}(Y = 1)\)
Find \(\mathbb{P}(Y \leq 2)\)

Joint distribution for two discrete random variables (4/5)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
- Find the joint CDF \(F_{X,Y}(x,y)\) for the joint pmf \(p_{X,Y}(x,y)\)

Joint distribution for two discrete random variables (5/5)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
- Find the marginal CDFs \(F_{X}(x)\) and \(F_{Y}(y)\)

Quick remarks on the joint and marginal CDF
\(F_X(x)\): right most columns of the CDF table (where the \(Y\) values are largest)
\(F_Y(y)\): bottom row of the table (where X values are largest)
\(F_X(x)=\lim\limits_{y\rightarrow\infty}F_{X, Y}(x,y)\)
\(F_Y(y)=\lim\limits_{x\rightarrow\infty}F_{X, Y}(x,y)\)
Learning Objectives
Define joint and marginal distributions for discrete and continuous random variables
Calculate or find joint and marginal probabilities, pmf’s, and CDF’s for discrete random variables
- Calculate or find joint and marginal probabilities, pdf’s, and CDF’s for continuous random variables
- Extra practice on your own: solve double integrals in a mini lesson
Common steps for joint pdfs and CDFs
- Set up the domain of the pdf with a picture
Translate to needed integrands
- For probability: shade in the area of interest, then translate
- For expected value: translate domain
- Set up integral: \(dxdy\) or \(dydx\)?
- Solve integral!
Example 2: Joint pdf (1/2)
Example 2.1
Let \(f_{X,Y}(x,y)= \frac32 y^2\), for \(0 \leq x \leq 2, \ 0 \leq y \leq 1\).
- Find \(\mathbb{P}(0 \leq X \leq 1, 0 \leq Y \leq \frac12)\)
Example 2: Joint pdf (2/2)
Example 2.2
Let \(f_{X,Y}(x,y)= \frac32 y^2\), for \(0 \leq x \leq 2, \ 0 \leq y \leq 1\).
- Find \(f_X(x)\) and \(f_Y(y)\).
Example with more complicated pdf (1/2)
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Example 3.1
Let \(f_{X,Y}(x,y)= 2 e^{-(x+y)}\), for \(0 \leq x \leq y\).
- Find \(f_X(x)\) and \(f_Y(y)\).
Example with more complicated pdf (2/2)
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Example 3.2
Let \(f_{X,Y}(x,y)= 2 e^{-(x+y)}\), for \(0 \leq x \leq y\).
- Find \(\mathbb{P}(Y < 3)\).
Recall: Finding the pdf of a transformation
Let \(M\) be a transformation of \(X\) and \(Y\): \(M = g(X, Y)\)
When we have a transformation of \(X\) and \(Y\), \(M\), we need to follow the CDF method to find the pdf of \(M\)
We follow CDF method:
Start with the joint pdf for \(X\) and \(Y\)
- aka \(f_{X,Y}(x, y)\)
Translate the domain of \(X\) and \(Y\) to \(M\): find possible values of \(M\)
Find the CDF of \(M\)
- aka \(F_M(m) = P(M \leq m) = P(g(X, Y) \leq m)\)
Take the derivative of the CDF of \(M\) with respect to \(m\) to find the pdf of \(M\)
- aka \(f_M(m) = \dfrac{d}{dm}F_M(m)\)
Example of a joint pdf with a transformation (1/3)
Example 4.1
Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).
- Find \(\mathbb{P}(|X-Y| < 2)\)
Example of a joint pdf with a transformation (2/3)
Example 4.2
Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).
- Let \(M = \max(X,Y)\). Find the pdf for \(M\), that is \(f_M(m)\)
Example of a joint pdf with a transformation (3/3)
Example 4.3
Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).
- Let \(Z = \min(X,Y)\). Find the pdf for \(Z\), that is \(f_Z(z)\).
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Last example for home: more complicated transformation
Example 5
Let \(X\) and \(Y\) have joint density \(f_{X,Y}(x,y)= \frac85(x+y)\) in the region \(0 < x < 1,\ \frac12 < y <1\). Find the pdf of the RV \(Z\), where \(Z=XY\).
Learning Objectives
Solve double integrals in our mini lesson!
Calculate probabilities for a pair of continuous random variables
Calculate a joint and marginal probability density function (pdf)
- Calculate a joint and marginal cumulative distribution function (CDF) from a pdf
Double Integrals Mini Lesson (1/3)
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Mini Lesson Example 1
Solve the following integral: \(\displaystyle\int_{2}^{3}\displaystyle\int_{0}^{1} xy dydx\)
Double Integrals Mini Lesson (2/3)
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Mini Lesson Example 2
Solve the following integral: \(\displaystyle\int_{2}^{3}\displaystyle\int_{0}^{1} (x+y) dydx\)
Double Integrals Mini Lesson (3/3)
Do this problem at home for extra practice. I’ll add the solution to the annotated notes!
Mini Lesson Example 3
Solve the following integral: \(\displaystyle\int_{2}^{3}\displaystyle\int_{0}^{1} e^{x+y} dydx\)
Lesson 11 Slides