Lesson 11: Joint distributions

Recall: Finding the pdf of a transformation

• Let \(M\) be a transformation of \(X\) and \(Y\): \(M = g(X, Y)\)

• When we have a transformation of \(X\) and \(Y\), \(M\), we need to follow the CDF method to find the pdf of \(M\)

We follow CDF method:

1. Start with the joint pdf for \(X\) and \(Y\)

   • aka \(f_{X,Y}(x, y)\)

2. Translate the domain of \(X\) and \(Y\) to \(M\): find possible values of \(M\)

3. Find the CDF of \(M\)

   • aka \(F_M(m) = P(M \leq m) = P(g(X, Y) \leq m)\)

4. Take the derivative of the CDF of \(M\) with respect to \(m\) to find the pdf of \(M\)

   • aka \(f_M(m) = \dfrac{d}{dm}F_M(m)\)

Example of a joint pdf with a transformation (1/3)

Example 4.1

Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).

1. Find \(\mathbb{P}(|X-Y| < 2)\)

Example of a joint pdf with a transformation (2/3)

Example 4.2

Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).

2. Let \(M = \max(X,Y)\). Find the pdf for \(M\), that is \(f_M(m)\)

\[ f_{X,Y}(x,y) = \dfrac{1}{16} \text{ for } 0 \leq x \leq 4, 0 \leq y \leq 4 \]

Plot of \(f_{X,Y}(x,y)\):

For first problem, we want:

Now I want to show the domain for the max, M:

Example of a joint pdf with a transformation (3/3)

Example 4.3

Let \(X\) and \(Y\) have constant density on the square \(0 \leq X \leq 4, 0 \leq Y \leq 4\).

3. Let \(Z = \min(X,Y)\). Find the pdf for \(Z\), that is \(f_Z(z)\).

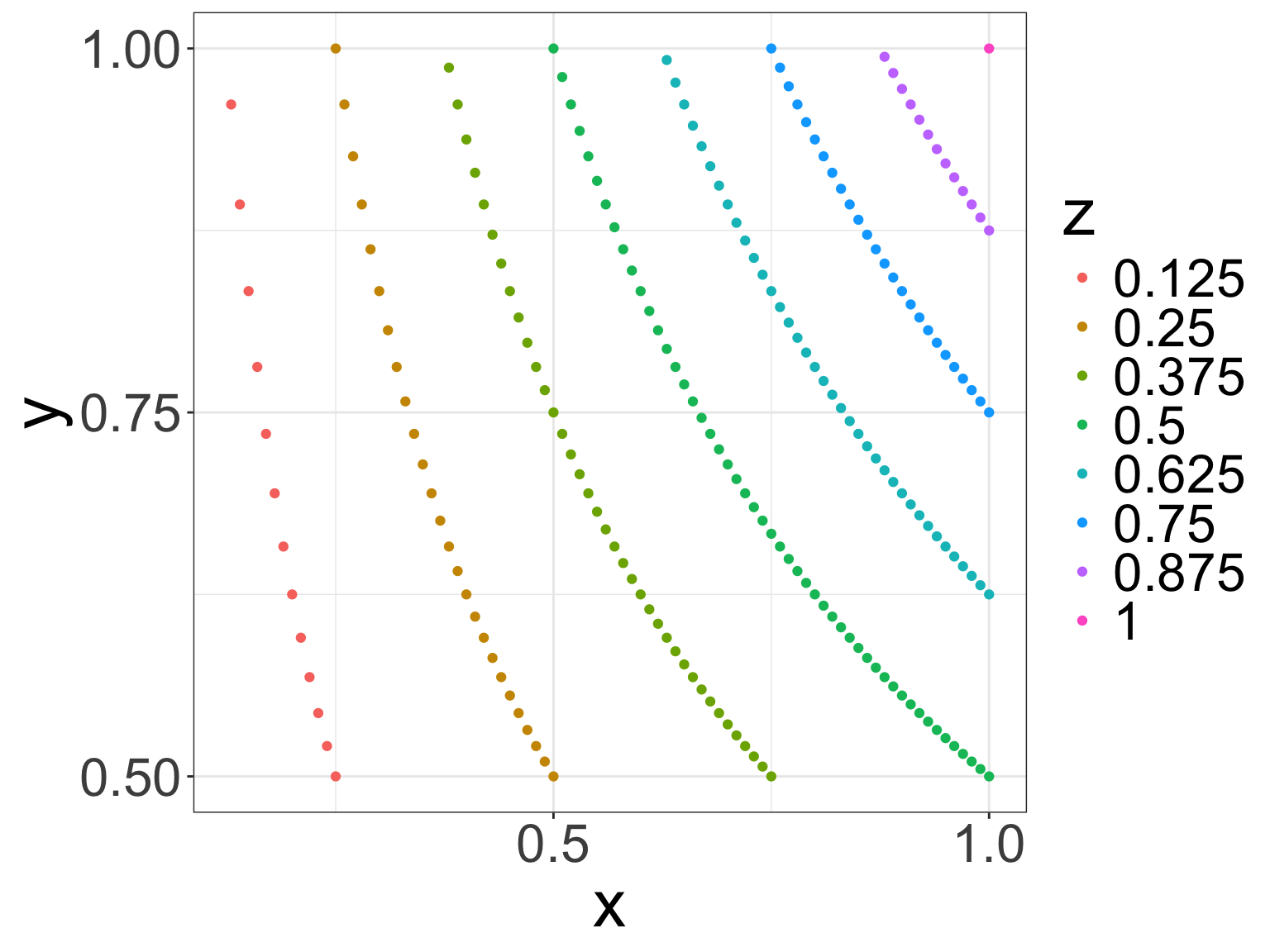
Last example for home: more complicated transformation

Example 5

Let \(X\) and \(Y\) have joint density \(f_{X,Y}(x,y)= \frac85(x+y)\) in the region \(0 < x < 1,\ \frac12 < y <1\). Find the pdf of the RV \(Z\), where \(Z=XY\).

We can look at the joint pdf of X and Y:

And let’s look at \(P(Z \leq 0.5)\) aka \(P(XY \leq 0.5)\) to get a better sense of the volume needed:

Now I want to show the domain for Z:

Now I want to show the domain for Z: