Lesson 12: Independence and Conditioning
2025-11-03
Learning Objectives
Identify the formula for joint distributions for independent RVs and conditional distributions (PMFs/PDFs)
Find conditional pmf from a joint pmf and check if two RVs are independent.
Construct a joint distribution for two independent continuous RVs from their marginal distributions.
Calculate conditional probabilities and distributions for continuous RVs.
Where are we?
Learning Objectives
- Identify the formula for joint distributions for independent RVs and conditional distributions (PMFs/PDFs)
Find conditional pmf from a joint pmf and check if two RVs are independent.
Construct a joint distribution for two independent continuous RVs from their marginal distributions.
Calculate conditional probabilities and distributions for continuous RVs.
How do we represent conditional pmfs/pdfs?
For events:
\[P(A | B) = \dfrac{P(A \cap B)}{P(B)}\]
For discrete RVs:
\[p_{X|Y}(x|y) = P(X=x|Y=y) = \dfrac{p_{X,Y}(x,y)}{p_Y(y)}\] \[p_{Y|X}(y|x) = P(Y=y|X=x) = \dfrac{p_{X,Y}(x,y)}{p_X(x)}\]
if denominator is greater than 0 (\(p_Y(y) > 0\) or \(p_X(x) > 0\))
For continuous RVs:
\[f_{X|Y}(x|y) = \dfrac{f_{X,Y}(x,y)}{f_Y(y)}\] \[f_{Y|X}(y|x) = \dfrac{f_{X,Y}(x,y)}{f_X(x)}\]
if denominator is greater than 0 (\(f_Y(y) > 0\) or \(f_X(x) > 0\))
How do we represent independent RVs in a joint pmf/pdf?
What do we know about independence for events?
For events: If \(A \perp B\)
\[P(A \cap B) = P(A)P(B)\] \[P(A|B) = P(A)\]
For discrete RVs: If \(X \perp Y\)
\[p_{X,Y}(x,y) = p_{X}(x)p_{Y}(y)\] \[F_{X,Y}(x,y) = F_{X}(x)F_{Y}(y)\] \[p_{X|Y}(x|y) = p_{X}(x)\] \[p_{Y|X}(y|x) = p_{Y}(y)\]
For continuous RVs: If \(X \perp Y\)
\[f_{X,Y}(x,y) = f_{X}(x)f_{Y}(y)\] \[F_{X,Y}(x,y) = F_{X}(x)F_{Y}(y)\] \[f_{X|Y}(x|y) = f_{X}(x)\] \[f_{Y|X}(y|x) = f_{Y}(y)\]
Remember: our probability rules must hold for these!
For discrete RVs
For a valid joint pmf, we need:
- \(0 \geq p_{X,Y}(x,y) \leq 1\) for all \(x, y\)
- \(\sum \limits_{\{all\ x\}} \sum \limits_{\{all\ y\}} p_{X,Y}(x,y)=1\)
For a valid conditional pmf, we need:
- \(0 \geq p_{X|Y}(x|y) \leq 1\) for all \(x, y\)
- \(\sum \limits_{\{all\ x\}} p_{X|Y}(x|y)=1\)
For continuous RVs
For a valid joint pdf, we need:
- \(f_{X,Y}(x,y)\geq 0\) for all \(x,y\)
- \(\displaystyle\int_{-\infty}^{\infty}\displaystyle\int_{-\infty}^{\infty} f_{X,Y}(x,y)dxdy=1\)
For a valid conditional pdf, we need:
- \(f_{X|Y}(x|y)\geq 0\) for all \(x\) and \(y\)
- \(\displaystyle\int_{-\infty}^{\infty} f_{X|Y}(x|y)dx =1\)
Extra notes
- If \(X_1, X_2, …, X_n\) are independent
\[p_{X_1, X_2, …, X_n}(x_1, x_2, …, x_n) = P(X_1=x_1, X_2=x_2, …, X_n=x_n)=\prod\limits_{i=1}^np_{X_i}(x_i)\] \[f_{X_1, X_2, …, X_n}(x_1, x_2, …, x_n) = \prod\limits_{i=1}^nf_{X_i}(x_i)\] \[F_{X_1, X_2, …, X_n}(x_1, x_2, …, x_n) = P(X_1\leq x_1, X_2\leq x_2, …, X_n\leq x_n)=\prod\limits_{i=1}^nP(X_i \leq x_i) = \prod\limits_{i=1}^nF_{X_i}(x_i)\]
- Don’t forget, you can manipulate the conditional density to get the joint: \[f_{X,Y}(x,y)= f_{X|Y}(x|y)f_Y(y)\]
Learning Objectives
- Identify the formula for joint distributions for independent RVs and conditional distributions (PMFs/PDFs)
- Find conditional pmf from a joint pmf and check if two RVs are independent.
Construct a joint distribution for two independent continuous RVs from their marginal distributions.
Calculate conditional probabilities and distributions for continuous RVs.
Last class: joint distribution for two discrete random variables (1/2)
Example 1
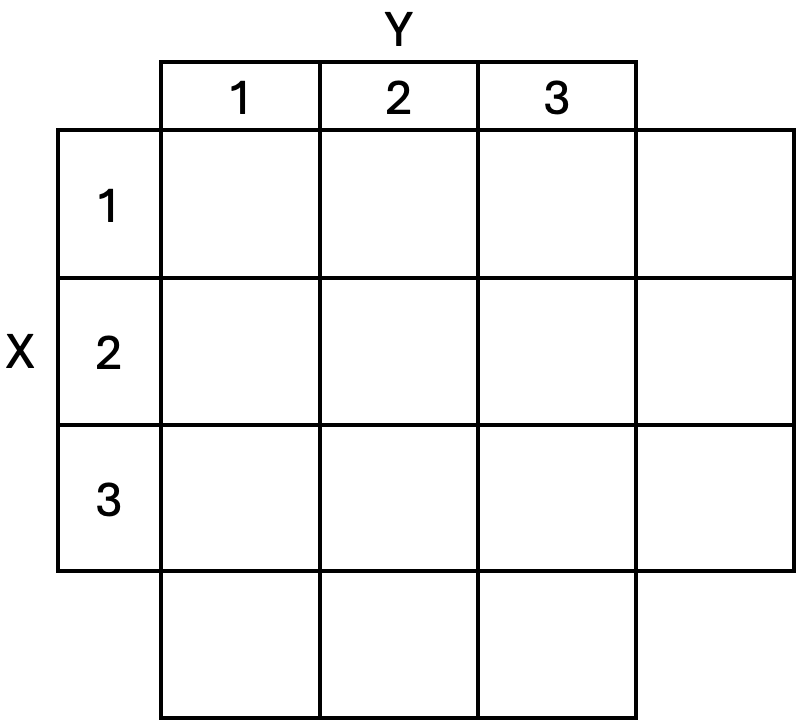
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
- Find \(p_{X|Y}(x|y)\).
Last class: joint distribution for two discrete random variables (2/2)
Example 1
Let \(X\) and \(Y\) be two random draws from a box containing balls labelled 1, 2, and 3 without replacement.
- Are \(X\) and \(Y\) independent? Why or why not?
Remark:
- To show that \(X\) and \(Y\) are not independent, we just need to find one counter example
- However, to show that they are independent, we need to verify this for all possible pairs of \(x\) and \(y\)

Learning Objectives
Identify the formula for joint distributions for independent RVs and conditional distributions (PMFs/PDFs)
Find conditional pmf from a joint pmf and check if two RVs are independent.
- Construct a joint distribution for two independent continuous RVs from their marginal distributions.
- Calculate conditional probabilities and distributions for continuous RVs.
Constructing a joint pdf from two independent, continuous RVs
Example 1.1
Let \(X\) and \(Y\) be independent r.v.’s with \(f_X(x)= \frac12\), for \(0 \leq x \leq 2\) and \(f_Y(y)= 3y^2\), for \(0 \leq y \leq 1\).
- Find \(f_{X,Y}(x,y)\)
Probability from joint pdf from two independent, continuous RVs
Example 1.2
Let \(X\) and \(Y\) be independent r.v.’s with \(f_X(x)= \frac12\), for \(0 \leq x \leq 2\) and \(f_Y(y)= 3y^2\), for \(0 \leq y \leq 1\).
- Find \(\mathbb{P}(0 \leq X \leq 1, 0 \leq Y \leq \frac12)\)
Showing independence from joint pdf
Example 2.1
Let \(f_{X,Y}(x,y)= 18 x^2 y^5\), for \(0 \leq x \leq 1, \ 0 \leq y \leq 1\).
- Are \(X\) and \(Y\) independent?
Finding CDF from two independent RVs
Example 2.2
Let \(f_{X,Y}(x,y)= 18 x^2 y^5\), for \(0 \leq x \leq 1, \ 0 \leq y \leq 1\).
- Find \(F_{X,Y}(x,y)\).
Showing independence from joint pdf
Do this problem at home for extra practice. The solution is available in Meike’s video!
Example 3
Let \(f_{X,Y}(x,y)= 2 e^{-(x+y)}\), for \(0 \leq x \leq y\). Are \(X\) and \(Y\) independent?
Final statement on independence
If \(f_{X,Y}(x,y)= g(x)h(y)\), where \(g(x)\) and \(h(y)\) are pdf’s, then \(X\) and \(Y\) are independent.
- The domain of the joint pdf needs to be independent as well!!
If \(F_{X,Y}(x,y)= G(x)H(y)\), where \(G(x)\) and \(H(y)\) are cdf’s, then \(X\) and \(Y\) are independent.
- The domain of the joint CDF needs to be independent as well!!
- Make sure that:
- \(X\) domain does NOT depend on \(Y\)
- \(Y\) domain does NOT depend on \(X\)
Learning Objectives
Identify the formula for joint distributions for independent RVs and conditional distributions (PMFs/PDFs)
Find conditional pmf from a joint pmf and check if two RVs are independent.
Construct a joint distribution for two independent continuous RVs from their marginal distributions.
- Calculate conditional probabilities and distributions for continuous RVs.
Example starting from a joint pdf: first try!
Example 1.1
Let \(f_{X,Y}(x,y)= 5 e^{-x-3y}\), for \(0 < y < \frac{x}{2}\).
- Find \(\mathbb{P}(2<X<10|Y=4)\)
Example starting from a joint pdf: second try! (1/2)
Example 1.1
Let \(f_{X,Y}(x,y)= 5 e^{-x-3y}\), for \(0 < y < \frac{x}{2}\).
- Find \(\mathbb{P}(2<X<10|Y=4)\)
Example starting from a joint pdf: second try! (2/2)
Example starting from a joint pdf
Do this problem at home for extra practice. The solution is available in Meike’s video!
Example 1.2
Let \(f_{X,Y}(x,y)= 5 e^{-x-3y}\), for \(0 < y < \frac{x}{2}\).
- Find \(\mathbb{P}(X>20 |Y=5)\)
Finding probability with conditional domain and pdf
Do this problem at home for extra practice. The solution is available in Meike’s video!
Example 2
Randomly choose a point \(X\) from the interval \([0,1]\), and given \(X=x\), randomly choose a point \(Y\) from \([0,x]\). Find \(\mathbb{P}(0 < Y < \frac14)\).
Lesson 12 Slides