Lesson 7: Data visualization of a single variable

Nicky Wakim

2024-10-21

Learning Objectives

1. Visualize distributions of numeric data/variables using histograms and boxplots

2. Recognize when transforming data helps make asymmetric data more symmetric (log values)

3. Visualize distributions of categorical data/variables using frequency tables and barplots

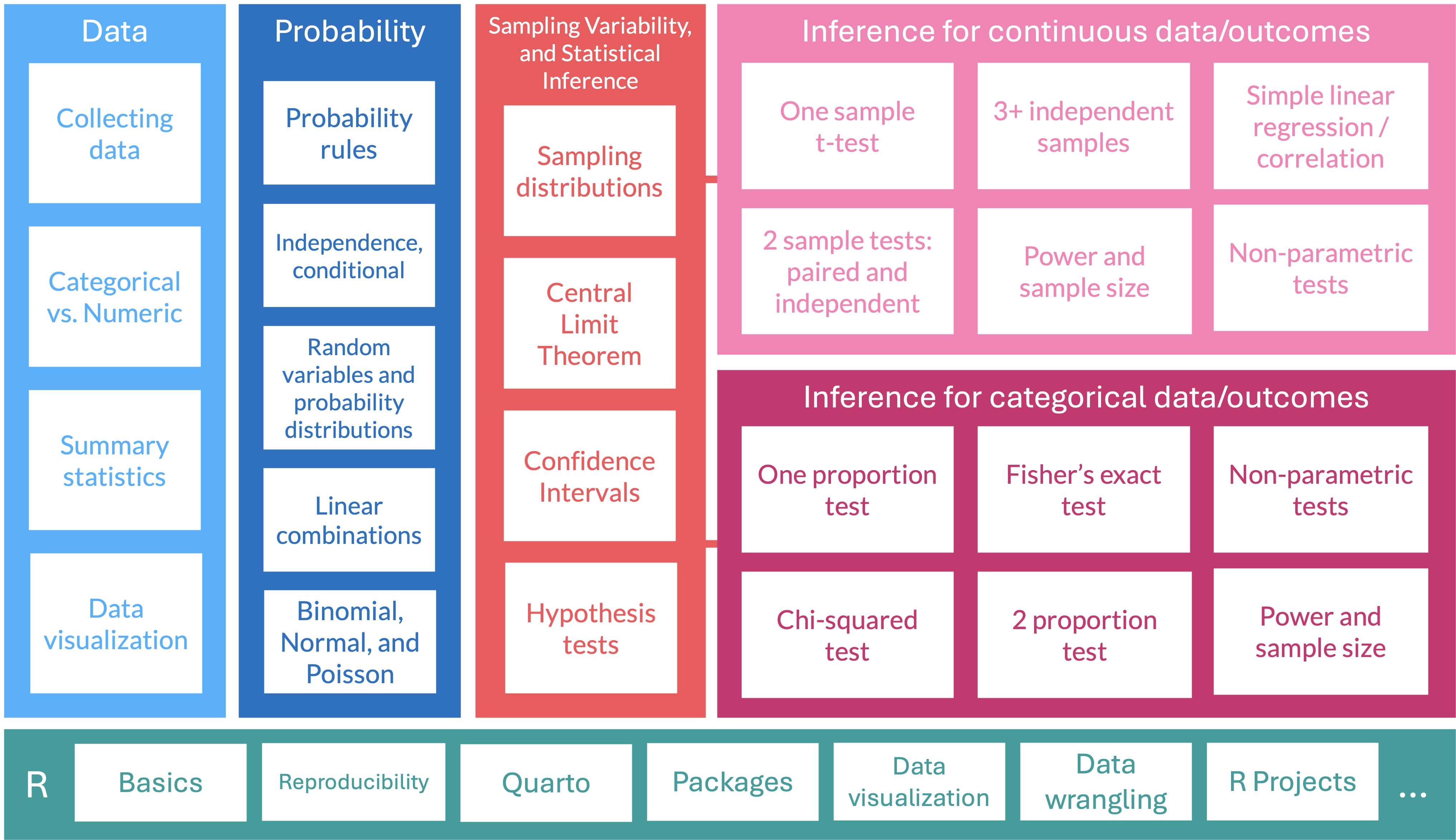
Where are we?

Artwork by @allison_horst

Why do we bother with visualizing data?¹

• Makes data easier to understand

  • helps you understand large amounts of data by turning it into a visual context, such as a graph or map

• Helps identify patterns

  • helps identify patterns, trends, and outliers in data sets. 

• Reveals data features

  • reveals data features that statistics and models might miss, such as unusual distributions, gaps, and outliers

• Helps with decision-making

  • helps with decision-making on analysis plans

1. Adapted from my Google search AI results: https://www.google.com/search?q=why+do+statistics+bother+with+data+visualization&rlz=1C5GCEM_enUS1130&oq=why+do+statistics+bother+with+data+visu&gs_lcrp=EgZjaHJvbWUqBwgBECEYoAEyBggAEEUYOTIHCAEQIRigATIHCAIQIRigATIHCAMQIRirAtIBCDk3NDBqMGo0qAIAsAIB&sourceid=chrome&ie=UTF-8

From Lesson 2: Example: the frog study¹

In evolutionary biology, parental investment refers to the amount of time, energy, or other resources devoted towards raising offspring.

 

We will be working with the frog dataset, which originates from a 2013 study² about maternal investment in a frog species. Reproduction is a costly process for female frogs, necessitating a trade-off between individual egg size and total number of eggs produced.

 

Researchers were interested in investigating how maternal investment varies with altitude. They collected measurements on egg clutches found at breeding ponds across 11 study sites; for 5 sites, the body size of individual female frogs was also recorded.

 

 

1. https://www.cdc.gov/nchs/products/databriefs/db220.htm

2. Chen, W., et al. Maternal investment increases with altitude in a frog on the Tibetan Plateau. Journal of evolutionary biology 26.12 (2013): 2710-2715.

From Lesson 2: Four rows from frog data frame

	altitude	latitude	egg.size	clutch.size	clutch.volume	body.size
1	3,462.00	34.82	1.95	181.97	177.83	3.63
2	3,462.00	34.82	1.95	269.15	257.04	3.63
3	3,462.00	34.82	1.95	158.49	151.36	3.72
150	2,597.00	34.05	2.24	537.03	776.25	NA

 

• Each row is an observation
• Each column is a variable
• All the observations and variables together make a data frame (sometimes called data matrix)

 

• Missing values: NA means the measured value for body size in clutch #150 is missing

From Lesson 2: Exploring data initially

• Techniques for exploring and summarizing data differ for numerical versus categorical variables.

 

• Numerical and graphical summaries are useful for examining variables one at a time
  • Can also be used for exploring the relationships between variables
  • Numerical summaries are not just for numerical variables (certain ones are used for categorical variables)

 

• Today we we look at ways to visualize a numerical variable and a categorical variable

Learning Objectives

1. Visualize distributions of numeric data/variables using histograms and boxplots

2. Recognize when transforming data helps make asymmetric data more symmetric (log values)

3. Visualize distributions of categorical data/variables using frequency tables and barplots

Histograms

• Histograms show the counts of observations (y-axis) that have values within a specific interval for a specific variable (x-axis)
• Show the shape of the distribution and data density
• Distribution is considered symmetric if the trailing parts of the plot are roughly equal
• Distribution is considered asymmetric if one tail trails off more than the other (as we see with clutch volume)
• Asymmetric distributions are said to be skewed
  • Skewed right if trails off to right
  • Skewed left if trails off to the left

Histograms

• Mode is represented by the tallest peak in the distribution
• When data have one prominent peak, we call it unimodel
• If there is more than one relative peak, we call it multimodel

Histograms

We can make a histogram of clutch volume or clutch size:

ggplot(data = frog, 
       aes(x = clutch.volume)) +
  geom_histogram() 

ggplot(data = frog, 
       aes(x = clutch.size)) +
  geom_histogram() 

Poll Everywhere Question 1

Boxplots

• A boxplot indicates the positions of the first, second, and third quartiles of a distribution in addition to extreme observations
• Interquartile range (IQR) represented by rectangle with black line through it for the median
• Whiskers extend from the box to capture data that are between \(Q_1\) and \(Q_1 - 1.5 IQR\) and separately between \(Q_3\) and \(Q_3 + 1.5 IQR\)
• An outlier is a value that appears extreme relative to the rest of the data
  • It is more than \(1.5IQR\) away from \(Q_1\) and \(Q_3\)

Boxplots

ggplot(data = frog, 
       aes(x = clutch.volume)) + 
  geom_boxplot() 

ggplot(data = frog, 
       aes(y = clutch.volume)) + 
  geom_boxplot() 

Learning Objectives

1. Visualize distributions of numeric data/variables using histograms and boxplots

2. Recognize when transforming data helps make asymmetric data more symmetric (log values)

3. Visualize distributions of categorical data/variables using frequency tables and barplots

We may want to transform data

• When working with strongly skewed data, it can be useful to apply a transformation

• Common to use the natural log transformation on skewed data

  • We typically just call this the “log transformation”

  • Especially for variables with many values clustered near 0 and other observations that are positive

• Transformations are mostly used when we make certain assumptions about the distribution of our data

  • For a lot of statistics methods, we assume the data is distributed normally
  • So we may need to transform the data to make it normal!

Let’s transform clutch volume!

ggplot(data = frog, 
       aes(x = clutch.volume)) +
  geom_histogram() 

ggplot(data = frog, 
       aes(x = log(clutch.volume))) +
  geom_histogram() 

Poll everywhere question 2

Learning Objectives

1. Visualize distributions of numeric data/variables using histograms and boxplots

2. Recognize when transforming data helps make asymmetric data more symmetric (log values)

3. Visualize distributions of categorical data/variables using frequency tables and barplots

From Lesson 4: Example: hypertension prevalence (1/2)

• US CDC estimated that between 2011 and 2014¹, 29% of the population in America had hypertension

 

• A health care practitioner seeing a new patient would expect a 29% chance that the patient might have hypertension
  • However, this is only the case if nothing else is known about the patient

1. https://www.cdc.gov/nchs/products/databriefs/db220.htm

From Lesson 4: Example: hypertension prevalence

• Prevalence of hypertension varies significantly with age
  • Among adults aged 18-39, 7.3% have hypertension
  • Adults aged 40-59, 32.2%
  • Adults aged 60 or older, 64.9% have hypertension

 

• Knowing the age of a patient provides important information about the likelihood of hypertension

  • Age and hypertension status are not independent (we will get into this)

• While the probability of hypertension of a randomly chosen adult is 0.29…

  • The conditional probability of hypertension in a person known to be 60 or older is 0.649

 

From Lesson 4: Contingency tables

• We can start looking at the contingency table for hypertension for different age groups
  • Contingency table: type of data table that displays the frequency distribution of two or more categorical variables

Table: Contingency table showing hypertension status and age group, in thousands.

Age Group	Hypertension	No Hypertension	Total
18-39 years	8836	112206	121042
40 to 59 years	42109	88663	130772
Greater than 60 years	39917	21589	61506
Total	90862	222458	313320

Let’s look at each variable separately

• The label “contingency tables” are usually reserved for when we have two variables in one table
• When we have one variable, we often call these frequency tables
  • Shows the count of observations that fall into a specific category
• In a relative frequency table, proportions for each category is shown instead of counts

Frequency table for age group variable

Age Group	Count
18-39 years	121042
40 to 59 years	130772
Greater than 60 years	61506
Total	313320

Relative frequency table for age group variable

Age Group	Count
18-39 years	0.3863
40 to 59 years	0.4174
Greater than 60 years	0.1963
Total	1.0000

Barplots

• A bar plot is a common way to display a single categorical variable
  • Show counts (or proportion) per category for a variable

ggplot(data = hyp_data, 
       aes(x = Age_Group)) + 
  geom_bar()

ggplot(data = hyp_data, 
       aes(x = Age_Group)) + 
  geom_bar(aes(y = stat(prop), 
               group = 1))

When to use what?

Variable type	Possible Visualizations	Nicky’s preferences
Numerical, discrete	histograms, boxplots	histograms
Numerical, continuous	histograms, boxplots	histograms
Categorical, ordinal	frequency tables, barplots	if I’m just looking: barplot if I’m writing a report: frequency table
Categorical, nominal	frequency tables, barplots	if I’m just looking: barplot if I’m writing a report: frequency table
Categorical, logical (binary)	frequency tables, barplots	frequency table or just a percent for one of the categories

Some notes about my visualization process

• If I am just looking at data alone, I use visualizations and summary statistics

  • I keep everything in its basic form without polishing the output

  • Plot labels are kept as variable name

  • I use a basic function like summary() to get

    • Mean and standard deviation for numeric variables

    • Counts for categorical variables

• If I am presenting visualizations or summary statistics, I will polish up everything

  • So that someone who is unfamiliar with the data can understand what I’m looking at

    • For example, I make sure variable names are written out and explained

 

• I want us to practice presenting visualizations, so I really want our homework visualizations to be polished