Lesson 11: Hypothesis Testing 1: Single-sample mean

TB sections 4.3, 5.1

Meike Niederhausen and Nicky Wakim

2024-11-06

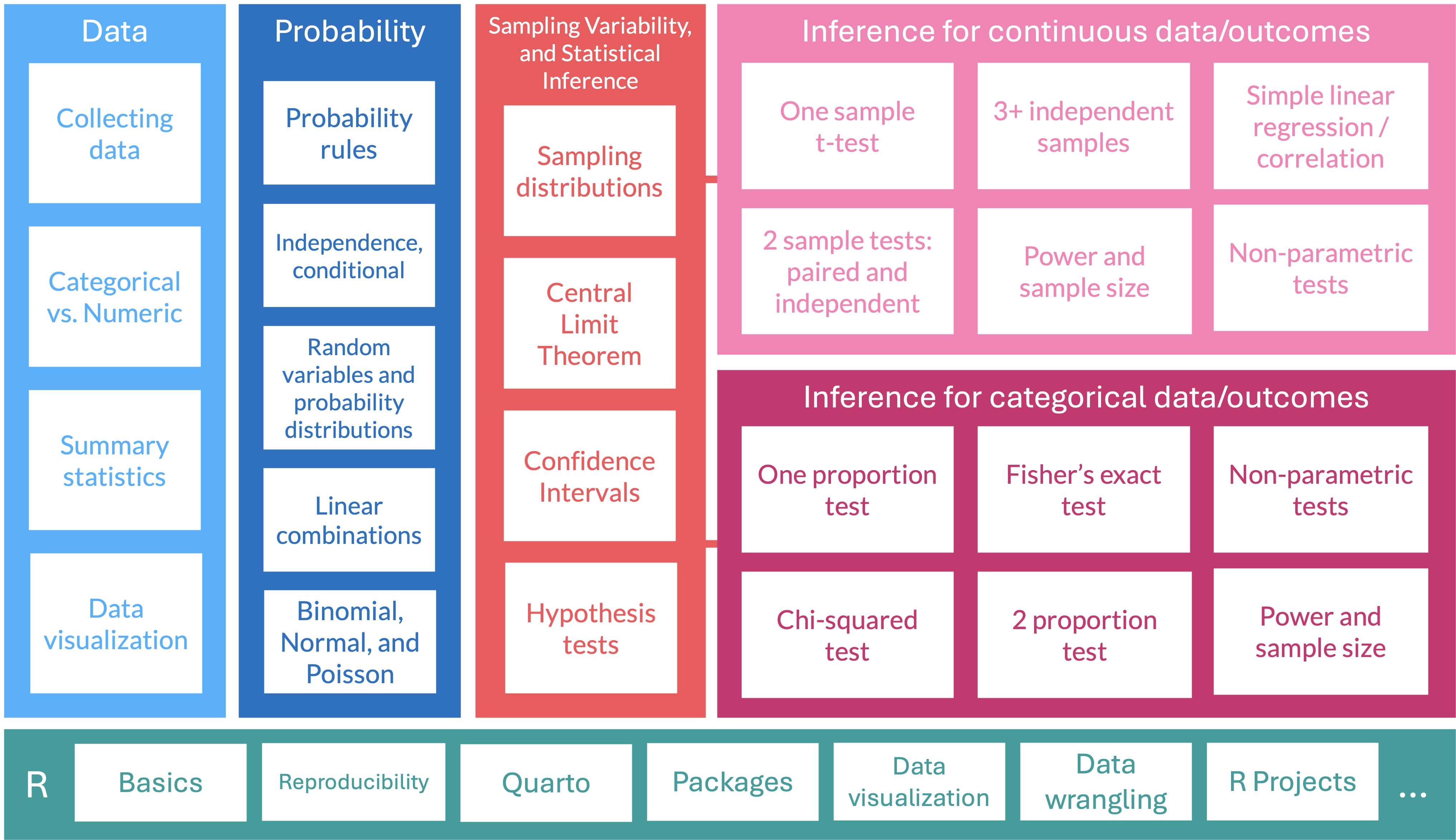
Where are we?

Learning Objectives

  1. Understand the relationship between point estimates, confidence intervals, and hypothesis tests.
  2. Determine if s single-sample mean is different than a population mean using a hypothesis test.
  3. Use R to calculate the test statistic, p-value, and confidence interval for a single-sample mean.

Learning Objectives

  1. Understand the relationship between point estimates, confidence intervals, and hypothesis tests.
  1. Determine if s single-sample mean is different than a population mean using a hypothesis test.
  2. Use R to calculate the test statistic, p-value, and confidence interval for a single-sample mean.

Answering a research question

Research question is a generic form: Is there evidence to support that the population mean is different than \(\mu\)?

 

Two approaches to answer this question:

Confidence interval

  • Create a confidence interval (CI) for the population mean \(\mu\) from our sample data and determine whether a prescribed value is inside the CI or not.
  • Answering the question: is \(\mu\) a plausible value given our data?

Hypothesis test

  • Run a hypothesis test to see if there is evidence that the population mean \(\mu\) is significantly different from a prescribed value
  • This does not give us a range of plausible values for the population mean \(\mu\).
  • Instead, we calculate a test statistic and p-value
  • See how likely we are to observe the sample mean \(\overline{x}\) or a more extreme sample mean assuming that the population mean \(\mu\) is a prescribed value

Last last time: Point estimates

Last time: Point estimates with their confidence intervals for \(\mu\)

 

Do these confidence intervals include \(\mu\)?

This time: Point estimates with probability assuming population mean \(\mu\)

 

Assuming the population mean is \(\mu\), what is the probability that we observe \(\overline{x}\) or a more extreme sample mean?

Last time: Confidence interval (CI) for the mean \(\mu\) (\(z\) vs. \(t\))

  • In summary, we have two cases that lead to different ways to calculate the confidence interval

Case 1: We know the population standard deviation

\[\overline{x}\ \pm\ z^*\times \text{SE}\]

  • with \(\text{SE} = \frac{\sigma}{\sqrt{n}}\) and \(\sigma\) is the population standard deviation

 

  • For 95% CI, we use:
    • \(z^* =\) qnorm(p = 0.975) \(=1.96\)

Case 2: We do not know the population sd

\[\overline{x}\ \pm\ t^*\times \text{SE}\]

  • with \(\text{SE} = \frac{s}{\sqrt{n}}\) and \(s\) is the sample standard deviation

 

  • For 95% CI, we use:
    • \(t^* =\) qt(p = 0.975, df = n-1)

Poll Everywhere Question 1

This time: Hypothesis test (\(z\) vs. \(t\))

  • We have two different distributions from which we run a hypothesis test

Case 1: We know the population standard deviation

  • We use a test statistic from a Normal distribution: \[z_{\overline{x}} = \dfrac{\overline{x} - \mu}{SE}\]

  • with \(\text{SE} = \frac{\sigma}{\sqrt{n}}\) and \(\sigma\) is the population standard deviation

Case 2: We do not know the population sd

  • We use a test statistic from a Student’s t-distribution: \[t_{\overline{x}} = \dfrac{\overline{x} - \mu}{SE}\]

  • with \(\text{SE} = \frac{s}{\sqrt{n}}\) and \(\sigma\) is the sample standard deviation

 

  • This is usually the case in real life

Is 98.6°F really the mean “healthy” body temperature?

Question: based on the 1992 JAMA data, is there evidence to support that the population mean body temperature is different from 98.6°F?

Question: based on the 1992 JAMA data, is there evidence to support that the population mean body temperature is different from 98.6°F?

Two approaches to answer this question:

Confidence interval

  • Create a confidence interval (CI) for the population mean \(\mu\) and determine whether 98.6°F is inside the CI or not.
  • Answering the question: is 98.6°F a plausible value?

Hypothesis test

  • Run a hypothesis test to see if there is evidence that the population mean \(\mu\) is significantly different from 98.6°F or not
  • This does not give us a range of plausible values for the population mean \(\mu\).
  • Instead, we calculate a test statistic and p-value
  • See how likely we are to observe the sample mean \(\overline{x}\) or a more extreme sample mean assuming that the population mean \(\mu\) is 98.6°F

Approach 1: Create a 95% CI for the population mean body temperature

  • Use data based on the results from the 1992 JAMA study
    • The original dataset used in the JAMA article is not available
    • However, Allen Shoemaker from Calvin College created a dataset with the same summary statistics as in the JAMA article, which we will use:

\[\overline{x} = 98.25,~s=0.733,~n=130\]

CI for \(\mu\): \[\begin{align} \overline{x} &\pm t^*\cdot\frac{s}{\sqrt{n}}\\ 98.25 &\pm 1.979\cdot\frac{0.733}{\sqrt{130}}\\ 98.25 &\pm 0.127\\ (98.123&, 98.377) \end{align}\]

 

Used \(t^*\) = qt(.975, df=129) = 1.979

 

Conclusion: We are 95% confident that the (population) mean body temperature is between 98.123°F and 98.377°F, which is discernably different than 98.6°F.

Approach 2: Hypothesis Test

From before:

  • Run a hypothesis test to see if there is evidence that the population mean \(\mu\) is significantly different from 98.6°F or not.

    • This does not give us a range of plausible values for the population mean \(\mu\).

    • Instead, we calculate a test statistic and p-value

      • to see how likely we are to observe the sample mean \(\overline{x}\)
      • or a more extreme sample mean
      • assuming that the population mean \(\mu\) is 98.6°F.

How do we calculate a test statistic and p-value?

  • Use the sampling distribution and central limit theorem!!
  • Focus on Case 2: we don’t know the population sd \(\sigma\)

Learning Objectives

  1. Understand the relationship between point estimates, confidence intervals, and hypothesis tests.
  1. Determine if s single-sample mean is different than a population mean using a hypothesis test.
  1. Use R to calculate the test statistic, p-value, and confidence interval for a single-sample mean.

Steps in a Hypothesis Test

  1. Check the assumptions

  2. Set the level of significance \(\alpha\)

  3. Specify the null ( \(H_0\) ) and alternative ( \(H_A\) ) hypotheses

    1. In symbols
    2. In words
    3. Alternative: one- or two-sided?

  4. Calculate the test statistic.

  5. Calculate the p-value based on the observed test statistic and its sampling distribution

  6. Write a conclusion to the hypothesis test

    1. Do we reject or fail to reject \(H_0\)?
    2. Write a conclusion in the context of the problem

Step 1: Check the assumptions

  • The assumptions to run a hypothesis test on a sample are:

    • Independent observations: the observations were collected independently.
    • Approximately normal sample or big n: the distribution of the sample should be approximately normal, or the sample size should be at least 30

 

  • These are the criteria for the Central Limit Theorem in Lesson 09: Variability in estimates

 

  • In our example, we would check the assumptions with a statement:

    • The individual observations are independent and the number of individuals in our sample is 130. Thus, we can use CLT to approximate the sampling distribution.

Step 2: Set the level of significance \(\alpha\)

  • Before doing a hypothesis test, we set a cut-off for how small the \(p\)-value should be in order to reject \(H_0\).

  • It is important to specify how rare or unlikely an event must be in order to represent sufficient evidence against the null hypothesis.

  • We call this the significance level, denoted by the Greek symbol alpha ( \(\alpha\) )

    • Typically choose \(\alpha = 0.05\)

  • This is parallel to our confidence interval

    • \(\alpha\) is the probability of rejecting the null hypothesis when it is true (it’s a measure of potential error)
    • From repeated (\(1-\alpha\))% confidence intervals, we will have about \(\alpha\)% intervals that do not cover \(\mu\) even though they come from the distribution with mean \(\mu\)

Step 3: Null & Alternative Hypotheses (1/2)

In statistics, a hypothesis is a statement about the value of an unknown population parameter.

A hypothesis test consists of a test between two competing hypotheses:

  1. a null hypothesis \(H_0\) (pronounced “H-naught”) vs.
  2. an alternative hypothesis \(H_A\) (also denoted \(H_1\))

Example of hypotheses in words:

\[\begin{aligned} H_0 &: \text{The population mean body temperature is 98.6°F}\\ \text{vs. } H_A &: \text{The population mean body temperature is not 98.6°F} \end{aligned}\]
  1. \(H_0\) is a claim that there is “no effect” or “no difference of interest.”
  2. \(H_A\) is the claim a researcher wants to establish or find evidence to support. It is viewed as a “challenger” hypothesis to the null hypothesis \(H_0\)

Step 3: Null & Alternative Hypotheses (2/2)

Notation for hypotheses

\[\begin{aligned} H_0 &: \mu = \mu_0\\ \text{vs. } H_A&: \mu \neq, <, \textrm{or}, > \mu_0 \end{aligned}\]

Hypotheses test for example

\[\begin{aligned} H_0 &: \mu = 98.6\\ \text{vs. } H_A&: \mu \neq 98.6 \end{aligned}\]

We call \(\mu_0\) the null value (hypothesized population mean from \(H_0\))

\(H_A: \mu \neq \mu_0\)

  • not choosing a priori whether we believe the population mean is greater or less than the null value \(\mu_0\)

\(H_A: \mu < \mu_0\)

  • believe the population mean is less than the null value \(\mu_0\)

\(H_A: \mu > \mu_0\)

  • believe the population mean is greater than the null value \(\mu_0\)
  • \(H_A: \mu \neq \mu_0\) is the most common option, since it’s the most conservative

Poll Everywhere Question 2

Step 4: Test statistic (& its distribution)

Case 1: We know the population standard deviation

  • We use a test statistic from a Normal distribution: \[z_{\overline{x}} = \dfrac{\overline{x} - \mu}{SE}\]

  • with \(\text{SE} = \frac{\sigma}{\sqrt{n}}\) and \(\sigma\) is the population standard deviation

  • Statistical theory tells us that \(z_{\overline{x}}\) follows a Standard Normal distribution \(N(0,1)\)

Case 2: We do not know the population sd

  • We use test statistic from Student’s t-distribution: \[t_{\overline{x}} = \dfrac{\overline{x} - \mu}{SE}\]

  • with \(\text{SE} = \frac{s}{\sqrt{n}}\) and \(\sigma\) is the sample standard deviation

  • Statistical theory tells us that \(t_{\overline{x}}\) follows a Student’s t distribution with degrees of freedom (df) = \(n-1\)

\(\overline{x}\) = sample mean, \(\mu_0\) = hypothesized population mean from \(H_0\),
\(\sigma\) = population standard deviation, \(s\) = sample standard deviation,
\(n\) = sample size

Step 4: Test statistic calculation

From our example: Recall that \(\overline{x} = 98.25\), \(s=0.733\), and \(n=130\)

The test statistic is:

\[t_{\overline{x}} = \frac{\overline{x} - \mu_0}{\frac{s}{\sqrt{n}}} = \frac{98.25 - 98.6}{\frac{0.73}{\sqrt{130}}} = -5.45\]

  • Statistical theory tells us that \(t_{\overline{x}}\) follows a Student’s t-distribution with \(df = n-1 = 129\)

Step 5: p-value

The p-value is the probability of obtaining a test statistic just as extreme or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true.

 

  • The \(p\)-value is a quantification of “surprise”
    • Assuming \(H_0\) is true, how surprised are we with the observed results?
    • Ex: assuming that the true mean body temperature is 98.6°F, how surprised are we to get a sample mean of 98.25°F (or more extreme)?

 

  • If the \(p\)-value is “small,” it means there’s a small probability that we would get the observed statistic (or more extreme) when \(H_0\) is true.

Step 5: p-value calculation

Calculate the p-value using the Student’s t-distribution with \(df = n-1 = 130-1=129\):

\[\text{p-value}=P(T \leq -5.45) + P(T \geq 5.45) = 2.410889 \times 10^{-07}\]

# use pt() instead of pnorm()
# need to specify df
2*pt(-5.4548, df = 130-1, lower.tail = TRUE)
[1] 2.410889e-07

Step 6: Conclusion to hypothesis test

\[\begin{aligned} H_0 &: \mu = \mu_0\\ \text{vs. } H_A&: \mu \neq \mu_0 \end{aligned}\]
  • Need to compare p-value to our selected \(\alpha = 0.05\)
  • Do we reject or fail to reject \(H_0\)?


If \(\text{p-value} < \alpha\), reject the null hypothesis

  • There is sufficient evidence that the (population) mean body temperature is discernibly different from \(\mu_0\) ( \(p\)-value = ___)
  • The average (insert measure) in the sample was \(\overline{x}\) (95% CI , ), which is discernibly different from \(\mu_0\) ( \(p\)-value = ____).

If \(\text{p-value} \geq \alpha\), fail to reject the null hypothesis

  • There is insufficient evidence that the (population) mean body temperature is discernibly different from \(\mu_0\) ( \(p\)-value = ___)
  • The average (insert measure) in the sample was \(\overline{x}\) (95% CI , ), which is not discernibly different from \(\mu_0\) ( \(p\)-value = ____).

Step 6: Conclusion to hypothesis test

\[\begin{aligned} H_0 &: \mu = 98.6\\ \text{vs. } H_A&: \mu \neq 98.6 \end{aligned}\]

  • Recall the \(p\)-value = \(2.410889 \times 10^{-07}\)

  • Need to compare back to our selected \(\alpha = 0.05\)

  • Do we reject or fail to reject \(H_0\)?

Conclusion statement:

  • Basic: (“stats class” conclusion)
    • There is sufficient evidence that the (population) mean body temperature is discernibly different from 98.6°F ( \(p\)-value < 0.001).
  • Better: (“manuscript style” conclusion)
    • The average body temperature in the sample was 98.25°F (95% CI 98.12, 98.38°F), which is discernibly different from 98.6°F ( \(p\)-value < 0.001).

Poll Everywhere Question 3

Learning Objectives

  1. Understand the relationship between point estimates, confidence intervals, and hypothesis tests.
  2. Determine if s single-sample mean is different than a population mean using a hypothesis test.
  1. Use R to calculate the test statistic, p-value, and confidence interval for a single-sample mean.

Load the dataset

  • The data are in a csv file called BodyTemperatures.csv
library(here)   # first install this package

BodyTemps <- read.csv(here::here("data", "BodyTemperatures.csv"))
#                     location: look in "data" folder
#                               for the file "BodyTemperatures.csv"

glimpse(BodyTemps)
Rows: 130
Columns: 3
$ Temperature <dbl> 96.3, 96.7, 96.9, 97.0, 97.1, 97.1, 97.1, 97.2, 97.3, 97.4…
$ Gender      <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
$ HeartRate   <int> 70, 71, 74, 80, 73, 75, 82, 64, 69, 70, 68, 72, 78, 70, 75…

t.test: base R’s function for testing one mean

  • Use the body temperature example with \(H_A: \mu \neq 98.6\)
  • We called the dataset BodyTemps when we loaded it
(temps_ttest <- t.test(x = BodyTemps$Temperature,
       alternative = "two.sided", # default setting
       mu = 98.6))

    One Sample t-test

data:  BodyTemps$Temperature
t = -5.4548, df = 129, p-value = 2.411e-07
alternative hypothesis: true mean is not equal to 98.6
95 percent confidence interval:
 98.12200 98.37646
sample estimates:
mean of x 
 98.24923

Note that the test output also gives the 95% CI using the t-distribution.

tidy() the t.test output

  • Use the tidy() function from the broom package for briefer output in table format that’s stored as a tibble
  • Combined with the gt() function from the gt package, we get a nice table
tidy(temps_ttest) %>% 
  gt() %>% 
  tab_options(table.font.size = 40) # use a different size in your HW
estimate statistic p.value parameter conf.low conf.high method alternative
98.24923 -5.454823 2.410632e-07 129 98.122 98.37646 One Sample t-test two.sided
  • Since the tidy() output is a tibble, we can easily pull() specific values from it:

Using base R’s $

tidy(temps_ttest)$p.value  
[1] 2.410632e-07

What’s next?

CI’s and hypothesis testing for different scenarios:

Lesson Section Population parameter Symbol (pop) Point estimate Symbol (sample)
11 5.1 Pop mean \(\mu\) Sample mean \(\overline{x}\)
12 5.2 Pop mean of paired diff \(\mu_d\) or \(\delta\) Sample mean of paired diff \(\overline{x}_{d}\)
13 5.3 Diff in pop means \(\mu_1-\mu_2\) Diff in sample means \(\overline{x}_1 - \overline{x}_2\)
15 8.1 Pop proportion \(p\) Sample prop \(\widehat{p}\)
15 8.2 Diff in pop prop’s \(p_1-p_2\) Diff in sample prop’s \(\widehat{p}_1-\widehat{p}_2\)

Reference: what does it all look like together?

Example of hypothesis test based on the 1992 JAMA data

Is there evidence to support that the population mean body temperature is different from 98.6°F?

  1. Assumptions: The individual observations are independent and the number of individuals in our sample is 130. Thus, we can use CLT to approximate the sampling distribution.

4-5.

  1. Set \(\alpha = 0.05\)

  1. Hypothesis:

    \[\begin{aligned} H_0 &: \mu = 98.6\\ \text{vs. } H_A&: \mu \neq 98.6 \end{aligned}\]
temps_ttest <- t.test(x = BodyTemps$Temperature, mu = 98.6)
tidy(temps_ttest) %>% gt() %>% tab_options(table.font.size = 36)
estimate statistic p.value parameter conf.low conf.high method alternative
98.24923 -5.454823 2.410632e-07 129 98.122 98.37646 One Sample t-test two.sided
  1. Conclusion: We reject the null hypothesis. The average body temperature in the sample was 98.25°F (95% CI 98.12, 98.38°F), which is discernibly different from 98.6°F ( \(p\)-value < 0.001).

Lesson 11 Slides