Lesson 15: Inference for a single proportion or difference of two (independent) proportions

TB sections 8.1-8.2

Meike Niederhausen and Nicky Wakim

2024-11-25

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion

  2. Run a hypothesis test for a single proportion and interpret the results.

  3. Construct and interpret confidence intervals for a single proportion.

  4. Understand how CLT applies to a difference in binomial random variables

  5. Run a hypothesis test for a difference in proportions and interpret the results.

  6. Construct and interpret confidence intervals for a difference in proportions.

Where are we?

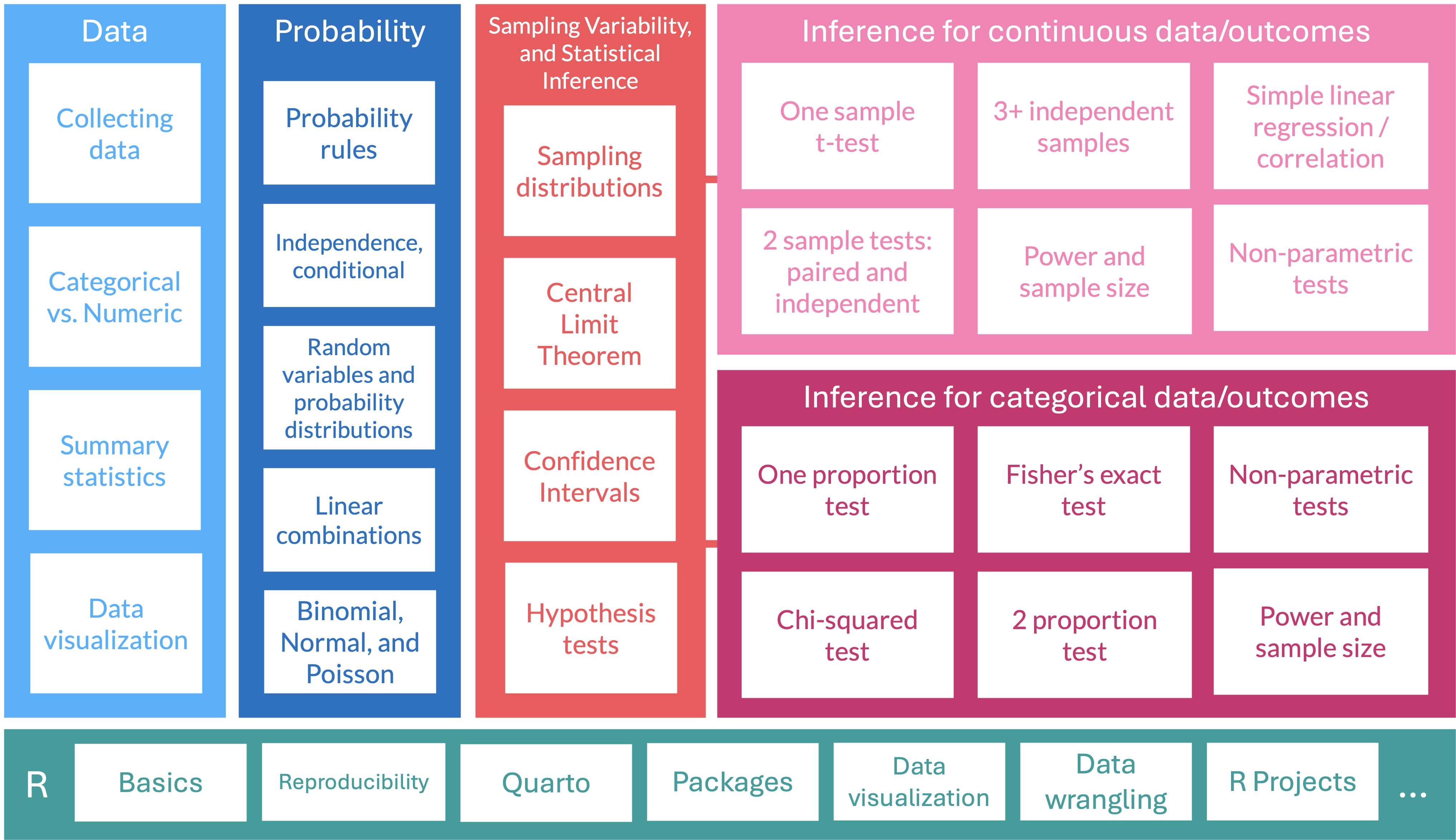
Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion

  1. Run a hypothesis test for a single proportion and interpret the results.

  2. Construct and interpret confidence intervals for a single proportion.

  3. Understand how CLT applies to a difference in binomial random variables

  4. Run a hypothesis test for a difference in proportions and interpret the results.

  5. Construct and interpret confidence intervals for a difference in proportions.

Moving to categorical outcomes

  • Previously, we have discussed methods of inference for numerical data

    • Our outcomes were numerical values
    • We were doing inference of means
    • We found confidence intervals for means
    • We ran hypothesis tests for means

 

  • Above methods used can be extended to categorical data, such as binomial proportions or data in two-way tables

 

  • Categorical data arise frequently in medical research

    • Disease outcomes and patient characteristics are often recorded in natural categories
    • Examples: types of treatment received, whether or not disease advanced to a later stage, or whether or not a patient responded initially to a treatment

From Lesson 5: Binomial random variable

  • One specific type of discrete random variable is a binomial random variable

Binomial random variable

  • \(X\) is a binomial random variable if it represents the number of successes in \(n\) independent replications (or trials) of an experiment where

    • Each replicate has two possible outcomes: either success or failure
    • The probability of success is \(p\)
    • The probability of failure is \(q=1-p\)

  • A binomial random variable takes on values \(0, 1, 2, \dots, n\).

  • If a r.v. \(X\) is modeled by a Binomial distribution, then we write in shorthand \(X \sim \text{Binom}(n,p)\)

  • Quick example: The number of heads in 3 tosses of a fair coin is a binomial random variable with parameters \(n = 3\) and \(p = 0.5\).

From Lesson 5: Binomial distribution

Distribution of a Binomial random variable

Let \(X\) be the total number of successes in \(n\) independent trials, each with probability \(p\) of a success. Then probability of observing exactly \(k\) successes in \(n\) independent trials is

\[P(X = x) = \binom{n}{x} p^x (1-p)^{n-x}, x= 0, 1, 2, \dots, n \]

  • The parameters of a binomial distribution are \(p\) and \(n\).

  • If a r.v. \(X\) is modeled by a binomial distribution, then we write in shorthand \(X \sim \text{Binom}(n,p)\)

Mean and variance of a Binomial r.v

If \(X\) is a binomial r.v. with probability of success \(p\), then \(E(X) = np\) and \(\text{Var}(X)=np(1-p)\)

From Lesson 6: Normal Approximation of the Binomial Distribution

  • Also known as: Sampling distribution of \(\widehat{p}\)

  • If \(X\sim \text{Binomial}(n,p)\) and \(np>10\) and \(nq = n(1-p) > 10\)

    • Ensures sample size (\(n\)) is moderately large and the \(p\) is not too close to 0 or 1
    • Other resources use other criteria (like \(npq>5\) or \(np>5\))

 

  • THEN approximately \[X\sim \text{Normal}\big(\mu_X = np, \sigma_X = \sqrt{np(1-p)} \big)\]

  • Continuity Correction: Applied to account for the fact that the binomial distribution is discrete, while the normal distribution is continuous

    • Adjust the binomial value (# of successes) by ±0.5 before calculating the normal probability.
    • For \(P(X \leq k)\) (Binomial), you would instead calculate \(P(X \leq k + 0.5)\) (Normal approx)
    • For \(P(X \geq k)\) (Binomial), you would instead calculate \(P(X \leq k - 0.5)\) (Normal approx)

Poll Everywhere Question 1

Sampling distribution of \(\hat{p}\)

  • \(\hat{p}=\frac{X}{n}\) where \(X\) is the number of “successes” and \(n\) is the sample size.
  • \(X \sim Bin(n,p)\), where \(p\) is the population proportion.
  • For \(n\) “big enough”, the normal distribution can be used to approximate a binomial distribution:

\[X \sim N\Big(\mu = np, \sigma = \sqrt{np(1-p)} \Big)\]

  • Since \(\hat{p}=\frac{X}{n}\) is a linear transformation of \(X\), we have for large n:

\[\hat{p} \sim N\Big(\mu_{\hat{p}} = p, \sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} \Big)\]

  • What is “big enough”? At least 10 successes and 10 failures are expected in the sample: \(np \geq 10\) and \(n(1-p) \geq 10\)

For proportions: Population parameters vs. sample statistics

Population parameter

  • Proportion: \(p\), \(\pi\) (“pi”)

Sample statistic (point estimate)

  • Sample proportion: \(\hat{p}\) (“p-hat”)

 

Approaches to answer a research question

  • Research question is a generic form for a single proportion: Is there evidence to support that the population proportion is different than \(p_0\)?

Calculate CI for the proportion \(p\):

\[\hat{p} \pm z^* \cdot SE_{\hat{p}} = \hat{p} \pm z^* \cdot\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]

  • with \(z^*\) = z-score that aligns with specific confidence interval

Run a hypothesis test:

Hypotheses

\[\begin{align} H_0:& p = p_0 \\ H_A:& p \neq p_0 \\ (or&~ <, >) \end{align}\]

Test statistic

\[ z_{\hat{p}} = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0\cdot(1-p_0)}{n}}} \]

R code: 1- and 2-sample proportions tests

prop.test(x, 
          n, 
          p = NULL, 
          alternative = c("two.sided", "less", "greater"), 
          conf.level = 0.95, 
          correct = TRUE)
  • x: Counts of successes (can have one x or a vector of multiple x’s)
  • n: Number of trails (can have one n or a vector of multiple n’s)
  • p: Null value that we think the population proportion is
  • alternative: If alternative hypothesis is \(\neq\), \(<\), or \(>\)
    • Default is “two.sided” (\(\neq\))
  • conf.level = Confidence level (\(1-\alpha\))
    • Default is 0.05
  • correct: Continuity correction, whether we should use it or not
    • Default is TRUE (Nicky says keep it this way!)

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion
  1. Run a hypothesis test for a single proportion and interpret the results.

  1. Construct and interpret confidence intervals for a single proportion.

  2. Understand how CLT applies to a difference in binomial random variables

  3. Run a hypothesis test for a difference in proportions and interpret the results.

  4. Construct and interpret confidence intervals for a difference in proportions.

Example: immune response to advanced melanoma

  • Looking for therapies that trigger an immune response to advanced melanoma

  • In a study where 52 patients were treated concurrently with two new therapies, nivolumab and ipilimumab

    • 21 had an immune response.1

  • Outcome: whether or not each person has an immune response

Questions that can be addressed with inference…

  • What is the estimated population probability of immune response following concurrent therapy with nivolumab and ipilimumab? (calculate \(\hat{p}\))

  • What is the 95% confidence interval for the estimated population probability of immune response following concurrent therapy with nivolumab and ipilimumab? (95% CI of \(p\))

  • In previous studies, the proportion of patients responding to one of these agents was 30% or less. Do these results suggest that the probability of response to concurrent therapy is better than 0.30? (Hypothesis test of null of 0.3)

Reference: Steps in a Hypothesis Test

  1. Check the assumptions

  2. Set the level of significance \(\alpha\)

  3. Specify the null ( \(H_0\) ) and alternative ( \(H_A\) ) hypotheses

    1. In symbols
    2. In words
    3. Alternative: one- or two-sided?

  4. Calculate the test statistic.

  5. Calculate the p-value based on the observed test statistic and its sampling distribution

  6. Write a conclusion to the hypothesis test

    1. Do we reject or fail to reject \(H_0\)?
    2. Write a conclusion in the context of the problem

Step 1: Check the assumptions (easier to do after Step 3)

The sampling distribution of \(\hat{p}\) is approximately normal when

  1. The sample observations are independent, and

  2. At least 10 successes and 10 failures are expected in the sample: \(np_0 \geq 10\) and \(n(1-p_0) \geq 10\).

 

  • Since \(p\) is unknown, it is necessary to substitute \(p_0\) (the null value) for \(p\) when using the standard error to conduct hypothesis tests
    • Because we are assuming the standard error of the null hypothesis!

 

  • For the example, we have \(p_0 = 0.30\)
    • We check: \(n p_0 = 52 \cdot 0.3 = 15.6 > 10\)
    • We check: \(n (1- p_0) = 52 (1 -0.3)= 36.4 > 10\)

Step 2: Set the level of significance

  • Before doing a hypothesis test, we set a cut-off for how small the \(p\)-value should be in order to reject \(H_0\).

  • Typically choose \(\alpha = 0.05\)

 

  • See Lesson 11: Hypothesis Testing 1: Single-sample mean

Step 3: Null & Alternative Hypotheses (1/2)

Notation for hypotheses (for paired data)

\[\begin{aligned} H_0 &: p = p_0\\ \text{vs. } H_A&: p \neq, <, \textrm{or}, > p_0 \end{aligned}\]

Hypotheses test for example

\[\begin{aligned} H_0 &: p = 0.30\\ \text{vs. } H_A&: p \neq 0.30 \end{aligned}\]

We call \(p_0\) the null value (hypothesized population mean difference from \(H_0\))

\(H_A: p \neq p_0\)

  • not choosing a priori whether we believe the population proportion is greater or less than the null value \(p_0\)

\(H_A: p < p_0\)

  • believe the population proportion is less than the null value \(p_0\)

\(H_A: p > p_0\)

  • believe the population population proportion is greater than the null value \(p_0\)
  • \(H_A: p \neq p_0\) is the most common option, since it’s the most conservative

Step 3: Null & Alternative Hypotheses (2/2)

Null and alternative hypotheses in words and in symbols.

One sample test

  • \(H_0\): For individuals who have advanced melanoma and received a treatment of nivolumab and ipilimumab, the population proportion of immune response is 0.30

  • \(H_A\): For individuals who have advanced melanoma and received a treatment of nivolumab and ipilimumab, the population proportion of immune response is NOT 0.30

\[\begin{align} H_0:& p = 0.30\\ H_A:& p \neq 0.30\\ \end{align}\]

Step 4: Test statistic

Sampling distribution of \(\hat{p}\) if we assume \(H_0: p=p_0\) is true:

\[\hat{p} \sim N\left(\mu_{\hat{p}} = p, \sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} \right) \sim N\left( \mu_{\hat{p}}=p_0, \sigma_{\hat{p}}=\sqrt{\frac{p_0\cdot(1-p_0)}{n}} \right)\]

Test statistic for a one sample proportion test:

\[ \begin{aligned} \text{test stat} = & \frac{\text{point estimate}-\text{null value}}{SE}\\ z_{\hat{p}} = & \frac{\hat{p} - p_0}{\sqrt{\frac{p_0\cdot(1-p_0)}{n}}} \end{aligned} \]

Step 4: Test statistic

From our example: Recall that \(\hat{p} = \dfrac{21}{52}= 0.4038\), \(n=52\), and \(p_0 = 0.30\)

The test statistic is:

\[ \begin{align} z_{\hat{p}} &= \frac{\hat{p} - p_0}{\sqrt{\frac{p_0\cdot(1-p_0)}{n}}} = \frac{21/52 - 0.30}{\sqrt{\frac{0.30\cdot(1-0.30)}{52}}} = 1.6341143 \end{align} \]

  • Let’s see the z-score on a Z-distribution (Standard Normal curve)

Poll Everywhere Question 2

Step 5: p-value

The p-value is the probability of obtaining a test statistic just as extreme or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true.

Calculate the p-value:

\[\begin{align} 2 &\cdot P(\hat{p}> 0.404) \\ &= 2 \cdot P\left(Z_{\hat{p}} > \frac{0.404 - 0.30}{\sqrt{\frac{0.30\cdot(1-0.30)}{52}}}\right)\\ &=2 \cdot P(Z_{\hat{p}} > 1.634)\\ &= 0.1022348 \end{align}\]

2*pnorm(1.634, lower.tail = F)
[1] 0.1022589

Step 4-5: test statistic and p-value together using prop.test()

prop.test(x = 21, n = 52, p = 0.30, correct = T)

    1-sample proportions test with continuity correction

data:  21 out of 52, null probability 0.3
X-squared = 2.1987, df = 1, p-value = 0.1381
alternative hypothesis: true p is not equal to 0.3
95 percent confidence interval:
 0.2731269 0.5487141
sample estimates:
        p 
0.4038462
Tidying the output of prop.test() 
prop.test(x = 21, n = 52, p = 0.30, correct = T) %>% 
  tidy() %>% gt() %>% tab_options(table.font.size = 40)
estimate statistic p.value parameter conf.low conf.high method alternative
0.4038462 2.198718 0.1381256 1 0.2731269 0.5487141 1-sample proportions test with continuity correction two.sided
  • Note: We expect some differences between the test statistic and p-value calculated by hand vs. by R. R uses a slightly different method to calculate.

Step 6: Conclusion to hypothesis test

\[\begin{align} H_0:& p = 0.30\\ H_A:& p \neq 0.30\\ \end{align}\]

  • Recall the \(p\)-value = 0.1022348
  • Use \(\alpha\) = 0.05.
  • Do we reject or fail to reject \(H_0\)?

Conclusion statement:

  • Stats class conclusion
    • There is insufficient evidence that the (population) proportion of individuals who had an immune response is different than 0.30 ( \(p\)-value = 0.102).
  • More realistic manuscript conclusion:
    • In a sample of 52 individuals receiving treatment, 40.4% had an immune response, which is not different from 30% ( \(p\)-value = 0.102).

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion
  2. Run a hypothesis test for a single proportion and interpret the results.
  1. Construct and interpret confidence intervals for a single proportion.

  1. Understand how CLT applies to a difference in binomial random variables

  2. Run a hypothesis test for a difference in proportions and interpret the results.

  3. Construct and interpret confidence intervals for a difference in proportions.

Conditions for one proportion: test vs. CI

Confidence interval conditions

  1. Independent observations
    • The observations were collected independently.


  1. The number of successes and failures is at least 10:

\[n\hat{p} \ge 10, \ \ n(1-\hat{p})\ge 10\]

Hypothesis test conditions

  1. Independent observations
    • The observations were collected independently.


  1. The number of expected successes and expected failures is at least 10.

\[n p_0 \ge 10, \ \ n(1-p_0)\ge 10\]

95% CI for population proportion

What to use for SE in CI formula?

\[\hat{p} \pm z^* \cdot SE_{\hat{p}}\]

Sampling distribution of \(\hat{p}\):

\[\hat{p} \sim N\left(\mu_{\hat{p}} = p, \sigma_{\hat{p}} = \sqrt{\frac{p(1-p)}{n}} \right)\]

Problem: We don’t know what \(p\) is - it’s what we’re estimating with the CI.
Solution: approximate \(p\) with \(\hat{p}\):

\[SE_{\hat{p}} = \sqrt{\frac{\hat{p}(1-\hat{p})}{n}}\]

  • Note that I am not using a continuity correction here! This means our “by hand” calculation will be different than our R calculation
    • Using the continuity correction is more widely accepted
    • So I would suggest using R to calculate the confidence intervals when you can!

95% CI for population proportion of immune response by hand

95% CI for population mean difference \(p\):

\[\begin{align} \hat{p} &\pm z^* \cdot SE_{\hat{p}}\\ \hat{p} &\pm z^* \cdot \sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \\ 0.404 &\pm 1.96\cdot \sqrt{\frac{0.404(1-0.404)}{52}} \\ 0.404 &\pm 1.96\cdot 0.068\\ 0.404 &\pm 0.133\\ (0.27&, 0.537) \end{align}\]

Used \(z^*\) = qnorm(0.975) = 1.96

 

“By hand” Conclusion:
We are 95% confident that the (population) proportion of individuals with an immune response is between 0.27 and 0.537.

95% CI for population proportion of immune response using R

  • We can use R to get similar values
prop.test(x = 21, n = 52, conf.level = 0.95, correct = T)

    1-sample proportions test with continuity correction

data:  21 out of 52, null probability 0.5
X-squared = 1.5577, df = 1, p-value = 0.212
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.2731269 0.5487141
sample estimates:
        p 
0.4038462

R Conclusion:
We are 95% confident that the (population) proportion of individuals with an immune response is between 0.273 and 0.549.

  • Note: We expect some differences between the confidence interval calculated by hand vs. by R. R uses a slightly different method to calculate.

Break Time!

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion

  2. Run a hypothesis test for a single proportion and interpret the results.

  3. Construct and interpret confidence intervals for a single proportion.

  1. Understand how CLT applies to a difference in binomial random variables

  1. Run a hypothesis test for a difference in proportions and interpret the results.

  2. Construct and interpret confidence intervals for a difference in proportions.

Inference for difference of two independent proportions
\(\hat{p}_1-\hat{p}_2\)

  • For means, we went from inferences on single sample mean to inferences on difference in means from two independent samples

 

  • We can do the same thing for proportions

 

  • We will go from inferences on single sample proportion to inferences on difference in proportions from two independent samples

Poll Everywhere Question 3

For difference in proportions: Population parameters vs. sample statistics

Population parameter

  • Population 1 proportion: \(p_1\), \(\pi_1\) (“pi”)

  • Population 2 proportion: \(p_2\), \(\pi_2\) (“pi”)  

 

  • Difference in proportions: \(p_1 - p_2\)

Sample statistic (point estimate)

  • Sample 1 proportion: \(\hat{p}_1\), \(\hat{\pi}_1\) (“pi”)

  • Sample 1 proportion: \(\hat{p}_2\), \(\hat{\pi}_2\) (“pi”)  

 

  • Difference in proportions: \(\hat{p}_1 - \hat{p}_2\)

 

Sampling distribution of \(\hat{p}_1-\hat{p}_2\)

  • \(\hat{p}_1=\frac{X_1}{n_1}\) and \(\hat{p}_2=\frac{X_2}{n_2}\),
    • \(X_1\) & \(X_2\) are the number of “successes”
    • \(n_1\) & \(n_2\) are the sample sizes of the 1st & 2nd samples

 

  • Each \(\hat{p}\) can be approximated by a normal distribution, for “big enough” \(n\)
  • Since the difference of independent normal random variables is also normal, it follows that for “big enough” \(n_1\) and \(n_2\)

\[\hat{p}_1 - \hat{p}_2 \sim N \left(\mu_{\hat{p}_1 - \hat{p}_2} = p_1 - p_2, ~~ \sigma_{\hat{p}_1 - \hat{p}_2} = \sqrt{ \frac{p_1\cdot(1-p_1)}{n_1} + \frac{p_2\cdot(1-p_2)}{n_2}} \right)\]

  • What is “big enough”? At least 10 successes and 10 failures are expected in the sample: \(n_1p \geq 10\), \(n_1(1-p) \geq 10\), \(n_2p \geq 10\), and \(n_2(1-p) \geq 10\)

Approaches to answer a research question

  • Research question is a generic form for a single proportion: Is there evidence to support that the population proportions are different from each other?

Calculate CI for the proportion difference \(p_1 - p_2\):

\[\hat{p}_1 - \hat{p}_2 \pm z^* \cdot SE_{\hat{p}_1 - \hat{p}_2}\]

  • with \(z^*\) = z-score that aligns with specific confidence interval

Run a hypothesis test:

Hypotheses

\[\begin{align} H_0:& p_1 - p_2 = 0 \\ H_A:& p_1 - p_2 \neq 0 \\ (or&~ <, >) \end{align}\]

Test statistic

\[ z_{\hat{p}_1 - \hat{p}_2} = \frac{\hat{p}_1 - \hat{p}_2}{SE_{pool}} \]

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion

  2. Run a hypothesis test for a single proportion and interpret the results.

  3. Construct and interpret confidence intervals for a single proportion.

  4. Understand how CLT applies to a difference in binomial random variables

  1. Run a hypothesis test for a difference in proportions and interpret the results.
  1. Construct and interpret confidence intervals for a difference in proportions.

Motivating example: effectiveness of mammograms

A 30-year study to investigate the effectiveness of mammograms versus a standard non-mammogram breast cancer exam was conducted in Canada with 89,835 participants. Each person was randomized to receive either annual mammograms or standard physical exams for breast cancer over a 5-year screening period.

By the end of the 25-year follow-up period, 1,005 people died from breast cancer. The results are summarized in the following table.

Displaying the contingency table in R 
BC %>% tabyl(Group, Death) %>% 
  adorn_totals(where = c("row", "col")) %>% 
  gt() %>% 
  tab_stubhead(label = "Group") %>%
  tab_spanner(label = "Death from breast cancer?", 
              columns = c("Yes", "No")) %>%
  tab_options(table.font.size = 45)
Group
Death from breast cancer?
 Total
Yes No
Control Group 505 44405 44910
Mammogram Group 500 44425 44925
Total 1005 88830 89835

Reference: Steps in a Hypothesis Test

  1. Check the assumptions

  2. Set the level of significance \(\alpha\)

  3. Specify the null ( \(H_0\) ) and alternative ( \(H_A\) ) hypotheses

    1. In symbols
    2. In words
    3. Alternative: one- or two-sided?

  4. Calculate the test statistic.

  5. Calculate the p-value based on the observed test statistic and its sampling distribution

  6. Write a conclusion to the hypothesis test

    1. Do we reject or fail to reject \(H_0\)?
    2. Write a conclusion in the context of the problem

Before we start, we need to calculate the pooled proportion

  • Often, our null hypothesis is that the two proportions are equal
    • And that both populations are the same
  • Thus, we calculate a pooled proportion to represent the proportion under the null distribution

\[\text{pooled proportion} = \hat{p}_{pool} = \dfrac{\text{total number of successes} }{ \text{total number of cases}} = \frac{x_1+x_2}{n_1+n_2}\]

  • In this example:

\[\hat{p}_{pool} = \frac{x_1+x_2}{n_1+n_2} = \frac{500 + 505}{(500 + 44425) + (505 + 44405)} = 0.01119\]

Poll Everywhere Question 4

Step 1: Check the assumptions

Conditions:

  • Independent observations & samples
    • The observations were collected independently.
    • In particular, observations from the two groups weren’t paired in any meaningful way.
  • The number of expected successes and expected failures is at least 10 for each group - using the pooled proportion:
    • \(n_1\hat{p}_{pool} \ge 10, \ \ n_1(1-\hat{p}_{pool}) \ge 10\)
    • \(n_2\hat{p}_{pool} \ge 10, \ \ n_2(1-\hat{p}_{pool}) \ge 10\)

 

  • In the example, we check:
    • \(n_1\hat{p}_{pool}=44925 \cdot 0.0112 = 502.5839 \ge 10\)
    • \(n_1(1-\hat{p}_{pool})= 44925 (1-0.0112) = 44422.42 \ge 10\)
    • \(n_2\hat{p}_{pool}=44910 \cdot 0.0112 = 502.4161 \ge 10\)
    • \(n_2(1-\hat{p}_{pool})= 44910 (1-0.0112) = 44407.58 \ge 10\)

Step 3: Null and Alternative Hypothesis test

Two samples test

  • \(H_0\): The difference in population proportions of deaths from breast cancer among people who received annual mammograms and annual physical check-ups is 0.

  • \(H_A\): The difference in population proportions of deaths from breast cancer among people who received annual mammograms and annual physical check-ups is not 0.

\[\begin{align} H_0:& p_{mamm} - p_{ctrl} = 0\\ H_A:& p_{mamm} - p_{ctrl} \neq 0\\ \end{align}\]

Step 4: Test statistic (1/2)

Sampling distribution of \(\hat{p}_1 - \hat{p}_2\): \[\hat{p}_1 - \hat{p}_2 \sim N \left(\mu_{\hat{p}_1 - \hat{p}_2} = p_1 - p_2, ~~ \sigma_{\hat{p}_1 - \hat{p}_2} = \sqrt{ \frac{p_1\cdot(1-p_1)}{n_1} + \frac{p_2\cdot(1-p_2)}{n_2}} \right)\]

Since we assume \(H_0: p_1 - p_2 = 0\) is true, we “pool” the proportions of the two samples to calculate the SE:

\[\text{pooled proportion} = \hat{p}_{pool} = \dfrac{\text{total number of successes} }{ \text{total number of cases}} = \frac{x_1+x_2}{n_1+n_2}\]

Test statistic:

\[ \text{test statistic} = z_{\hat{p}_1 - \hat{p}_2} = \frac{\hat{p}_1 - \hat{p}_2 - 0}{\sqrt{\frac{\hat{p}_{pool}(1-\hat{p}_{pool})}{n_1} + \frac{\hat{p}_{pool}(1-\hat{p}_{pool})}{n_2}}} \]

Step 4: Test statistic (2/2)

From our example: Recall that \(\hat{p}_1 = \dfrac{500}{44925}= 0.0111\), \(\hat{p}_2 = \dfrac{505}{44910}= 0.0112\), \(n_1=44925\), \(n_2=44910\), and \(\hat{p}_{pool} = 0.01119\)

The test statistic is:

\[ \begin{align} z_{\hat{p}_1 - \hat{p}_2} = \frac{\hat{p}_1 - \hat{p}_2 - 0}{\sqrt{\frac{\hat{p}_{pool}\cdot(1-\hat{p}_{pool})}{n_1} + \frac{\hat{p}_{pool}\cdot(1-\hat{p}_{pool})}{n_2}}} = \frac{0.0111 -0.0112}{\sqrt{\frac{0.01119\cdot(1-0.01119)}{44925} + \frac{0.01119\cdot(1-0.01119)}{44910}}} = -0.163933 \end{align} \]

  • Let’s see the z-score on a Z-distribution (Standard Normal curve)

Step 5: p-value

The p-value is the probability of obtaining a test statistic just as extreme or more extreme than the observed test statistic assuming the null hypothesis \(H_0\) is true.

Calculate the p-value:

\[\begin{align} & 2 \cdot P(\hat{p}_1 - \hat{p}_2< 0.0111 - 0.0112) \\ &= P\left(Z_{\hat{p}_1 - \hat{p}_2} < \frac{0.0111 - 0.0112}{\sqrt{\frac{0.01119\cdot(1-0.01119)}{44925} + \frac{0.01119\cdot(1-0.01119)}{44910}}}\right) \\ &= 2 \cdot P(Z_{\hat{p}} > -0.164)\\ &= 0.8697839 \end{align}\]

2*pnorm(-0.1639)
[1] 0.8698099

Step 4-5: test statistic and p-value together using prop.test()

prop.test(x = c(505, 500), n = c(44910, 44925)) # no p needed

    2-sample test for equality of proportions with continuity correction

data:  c(505, 500) out of c(44910, 44925)
X-squared = 0.01748, df = 1, p-value = 0.8948
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.001282751  0.001512853
sample estimates:
    prop 1     prop 2 
0.01124471 0.01112966
Tidying the output of prop.test() 
prop.test(x = c(505, 500), n = c(44910, 44925)) %>% 
  tidy() %>% gt() %>% tab_options(table.font.size = 33)
estimate1 estimate2 statistic p.value parameter conf.low conf.high method alternative
0.01124471 0.01112966 0.01747975 0.8948174 1 -0.001282751 0.001512853 2-sample test for equality of proportions with continuity correction two.sided
  • Note: We expect some differences between the test statistic and p-value calculated by hand vs. by R. R uses a slightly different method to calculate.

Step 6: Conclusion to hypothesis test

\[\begin{align} H_0:& p_{mamm} - p_{ctrl} = 0\\ H_A:& p_{mamm} - p_{ctrl} \neq 0\\ \end{align}\]

  • Recall the \(p\)-value = 0.8698
  • Use \(\alpha\) = 0.05
  • Do we reject or fail to reject \(H_0\)?

Conclusion statement:

  • Stats class conclusion
    • There is insufficient evidence that the difference in (population) proportions of deaths from breast cancer among people who received annual mammograms and annual physical check-ups different (\(p\)-value = 0.87).
  • More realistic manuscript conclusion:
    • 1.11% of people receiving annual mammograms (n=44925) and 1.12% of people receiving annual physical exams (n=44925) died from breast cancer (\(p\)-value = 0.87).

Learning Objectives

  1. Remind ourselves of the Normal approximation of the binomial distribution and define the sampling distribution of a sample proportion

  2. Run a hypothesis test for a single proportion and interpret the results.

  3. Construct and interpret confidence intervals for a single proportion.

  4. Understand how CLT applies to a difference in binomial random variables

  5. Run a hypothesis test for a difference in proportions and interpret the results.

  1. Construct and interpret confidence intervals for a difference in proportions.

Conditions for difference in proportions: test vs. CI

Confidence interval conditions

  1. Independent observations & samples
    • The observations were collected independently.
    • In particular, observations from the two groups weren’t paired in any meaningful way.


  1. The number of successes and failures is at least 10 for each group.
    • \(n_1\hat{p}_1 \ge 10, \ \ n_1(1-\hat{p}_1) \ge 10\)
    • \(n_2\hat{p}_2 \ge 10, \ \ n_2(1-\hat{p}_2) \ge 10\)

Hypothesis test conditions

  1. Independent observations & samples
    • The observations were collected independently.
    • In particular, observations from the two groups weren’t paired in any meaningful way.


  1. The number of expected successes and expected failures is at least 10 for each group - using the pooled proportion:
    • \(n_1\hat{p}_{pool} \ge 10, \ \ n_1(1-\hat{p}_{pool}) \ge 10\)
    • \(n_2\hat{p}_{pool} \ge 10, \ \ n_2(1-\hat{p}_{pool}) \ge 10\)

Poll Everywhere Question 5

95% CI for population difference in proportions

What to use for SE in CI formula?

\[\hat{p}_1 - \hat{p}_2 \pm z^* \cdot SE_{\hat{p}_1 - \hat{p}_2}\]

SE in sampling distribution of \(\hat{p}_1 - \hat{p}_2\)

\[\sigma_{\hat{p}_1 - \hat{p}_2} = \sqrt{ \frac{p_1\cdot(1-p_1)}{n_1} + \frac{p_2\cdot(1-p_2)}{n_2}} \]

Problem: We don’t know what \(p\) is - it’s what we’re estimating with the CI.
Solution: approximate \(p_1\), \(p_2\) with \(\hat{p}_1\), \(\hat{p}_2\):

\[SE_{\hat{p}_1 - \hat{p}_2} = \sqrt{ \frac{\hat{p}_1\cdot(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2\cdot(1-\hat{p}_2)}{n_2}}\]

95% CI for the population difference in proportions

95% CI for population mean difference \(p_1 - p_2\):

\[\begin{align} \hat{p}_1 - \hat{p}_2 &\pm z^* \cdot SE_{\hat{p}_1 - \hat{p}_2}\\ \hat{p}_1 - \hat{p}_2 &\pm z^* \cdot \sqrt{ \frac{\hat{p}_1\cdot(1-\hat{p}_1)}{n_1} + \frac{\hat{p}_2\cdot(1-\hat{p}_2)}{n_2}} \\ 0.01113 - 0.01124 &\pm 1.96 \cdot \sqrt{\frac{0.01113\cdot(1-0.01113)}{44925} + \frac{0.01124\cdot(1-0.01124)}{44910}}\\ 0.35 &\pm 1.96\cdot 0.001\\ 0.35 &\pm 0.002\\ (-0.002&, 0.002) \end{align}\]

Used \(z^*\) = qnorm(0.975) = 1.96

 

Interpretation:
We are 95% confident that the difference in (population) proportions of deaths due to breast cancer comparing people who received annual mammograms to annual physical check-ups is between -0.002 and 0.002.

95% CI for the population difference in proportions

  • We can use R to get similar values
prop.test(x = c(505, 500), n = c(44910, 44925))

    2-sample test for equality of proportions with continuity correction

data:  c(505, 500) out of c(44910, 44925)
X-squared = 0.01748, df = 1, p-value = 0.8948
alternative hypothesis: two.sided
95 percent confidence interval:
 -0.001282751  0.001512853
sample estimates:
    prop 1     prop 2 
0.01124471 0.01112966

R Conclusion:
We are 95% confident that the difference in (population) proportions of deaths due to breast cancer comparing people who received annual mammograms to annual physical check-ups is between -0.0013 and 0.0015.

  • Note: We expect some differences between the confidence interval calculated by hand vs. by R. R uses a slightly different method to calculate.

Lesson 15 Slides