Lesson 17: Wrap-up and other regressions

Nicky Wakim

2024-06-05

Animals of the day

Today

  • Let’s zoom out a little and see what types of regressions we can do
  • You should have the main tools to perform these regressions
    • Each has some nuances, but I’ll give you sources that help walk you through them

Types of regressions

Dist’n of Y Typical uses Link name Link function Common name
Normal Linear-response data Identity \(g(\mu)=\mu\) Linear regression
Bernoulli / Binomial outcome of single yes/no occurrence Logit \(g(\mu)=\text{logit}(\mu)\) Logistic regression
Poisson count of occurrences in fixed amount of time/space Log \(g(\mu)=\log(\mu)\) Poisson regression
Bernoulli / Binomial outcome of single yes/no occurrence Log \(g(\mu)=\log(\mu)\) Log-binomial regression
Multinomial outcome of single occurence with K > 2 options, nominal Logit \(g(\mu)=\text{logit}(\mu)\) Multinomial logistic regression
Multinomial outcome of single occurence with K > 2 options, ordinal Logit \(g(\mu)=\text{logit}(\mu)\) Ordinal logistic regression

Linear regression

  • Outcome type: continuous

 

  • Example outcomes:
    • Height
    • IAT score
    • Heart rate
  • Population model

\[ E(Y \mid X) = \mu = \beta_0 + \beta_1 X\]

  • Interpretations
    • The change in average \(Y\) for every 1 unit increase in \(X\)

Linear regression resources

Logistic regression

  • Outcome type: binary, yes or no

 

  • Example outcomes:
    • Food insecurity
    • Disease diagnosis for patient
    • Fracture
  • Population model

\[ \text{logit}(\mu) = \beta_0 + \beta_1 X\]

  • Interpretations
    • The log-odds ratio for every 1 unit increase in \(X\)

Logistic regression resources

Poisson Regression

  • Outcome type: Counts or rates

 

  • Example outcomes:
    • Number of children in household
    • Number of hospital admissions
    • Rate of incidence for COVID in US counties
  • Population model

\[ \log(\mu) = \beta_0 + \beta_1 X\]

  • Interpretations
    • The count (or rate) ratio for every 1 unit increase in \(X\)

Poisson Regression resources

Log-binomial Regression

  • Outcome type: binary, yes or no

 

  • Example outcomes:
    • Food insecurity
    • Disease diagnosis for patient
    • Fracture
  • Population model

\[ \log(\mu) = \beta_0 + \beta_1 X\]

  • Interpretations
    • We have log of probability on the left
    • So exponential of our coefficients will be risk ratio

Log-binomial Regression resources

Multinomial logistic regression

  • Outcome type: multi-level categorical, no inherent order
  • Example outcomes:
    • Blood type
    • US region (from WBNS)
    • Primary site of lung cancer (upper lobe, lower lobe, overlapped, etc.)
  • We have additional restriction that the multiple group probabilities sum to 1

  • Population models\[ \log \left(\dfrac{\mu_{\text{group } 2}}{\mu_{\text{group } 1}} \right) = \beta_0 + \beta_1 X\] \[ \log \left(\dfrac{\mu_{\text{group } 3}}{\mu_{\text{group } 1}} \right) = \beta_0 + \beta_1 X\]

  • Interpretations

    • Basically fitting two binary logistic regressions at same time!
    • First equation: how a one unit change in \(X\) changes the log-odds of going from group 1 to group 2
    • Second equation: how a one unit change in \(X\) changes the log-odds of going from group 1 to group 3

Multinomial logistic regression resources

Ordinal logistic regression

  • Outcome type: multi-level categorical, with inherent order
  • Example outcomes:
    • Satisfaction level (likert scale)
    • Pain level
    • Stages of cancer

 

  • When these variables are predictors, we are pretty lenient about treating them as continuous
    • We must be VERY STRICT when they are outcomes
    • They do not meet the assumptions we place on continuous outcomes in linear regression!!
  • We have additional restriction that the multiple group probabilities sum to 1
  • Population models , with levels \(k = 1, 2, 3, ..., K\)

\[ \log \left(\dfrac{P(Y \leq 1)}{P(Y > 1)} \right) = \beta_0 + \beta_1 X\] \[ \log \left(\dfrac{P(Y \leq k)}{P(Y > k)} \right) = \beta_0 + \beta_1 X\]

  • Interpretations
    • Basically fitting \(K\) binary logistic regressions at same time!
    • First equation: how a one unit change in \(X\) changes the log-odds of going from group 1 to any other group
    • Second equation: how a one unit change in \(X\) changes the log-odds of going from group 1 or 2 to group 3 or above

Ordinal logistic regression resources

Even more regressions…

Dist’n of Y Typical uses Link name Link function Common name
Bernoulli / Binomial outcome of single yes/no occurrence Probit \(g(\mu)=\Phi^{-1}(\mu)\) Probit regression
Bernoulli / Binomial outcome of single yes/no occurrence Complementary log-log \(g(\mu)=\log(-\log(1-\mu))\) Complementary log-log regression
Multinomial outcome of single occurence with K > 2 options, nominal Probit \(g(\mu)=\Phi^{-1}(\mu)\) Multinomial probit regression
Multinomial outcome of single occurence with K > 2 options, ordinal Probit \(g(\mu)=\Phi^{-1}(\mu)\) Ordered probit regression

More regression resources

General resources

Moment of appreciation for your growth

  • Remember when we were learning simple linear regression…
  • This was a slide from our second week together:
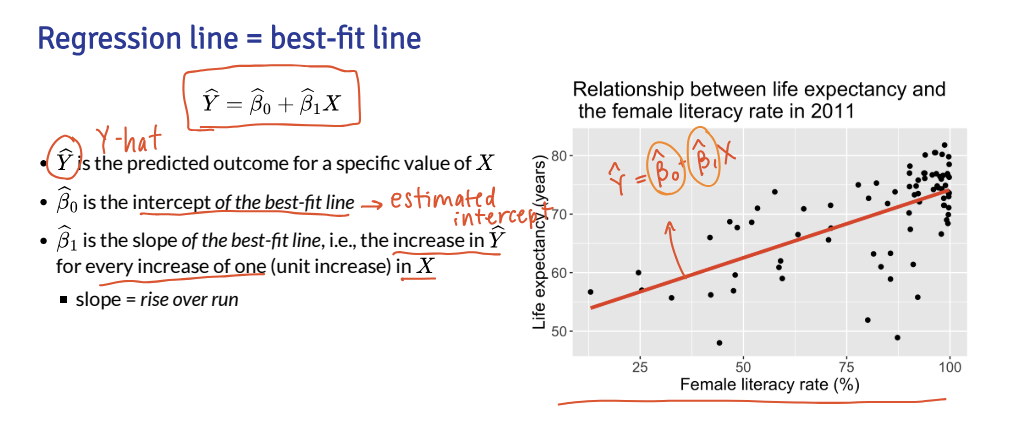
  • Even if you don’t feel like you learned everything, you have learned a lot from the first time you saw the above slide

Lesson 17: Wrap-up and other regressions