Muddy Points
Chapter 2: Probability
The muddy points from this year were a subset of the ones from last year, so I just decided to copy those below!
1. Proofs of propositions
Further explanations of the propositions can be found in the textbook from pages 24-27. For many of the explanations in class, I was working to produce a union of disjoint events, so that the probability could easily be calculated. Proposition 3 and 4 were specifically mentioned, so I will include some writing notes on them here:
Proposition 3
If \(A \subseteq B\), then \(\mathbb{P}(A) \leq \mathbb{P}(B)\)
In this proposition, I want to define event \(B\) as a union of disjoint events so that I can show \(P(B)\) is the sum of \(P(A)\) and some greater-than-or-equal-to 0 probability event. If the following is my venn diagram of A and B:
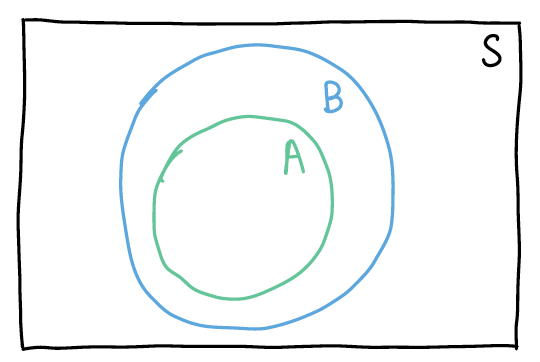
Then I can define B as the union of disjoint events: 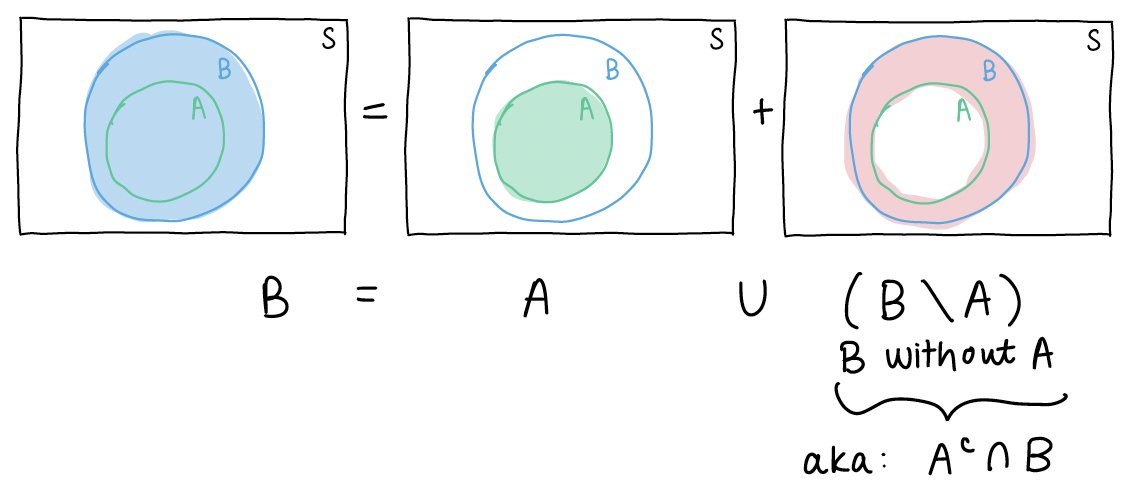
If we then take the probability of each side of the equation \(B = A \cup (A^c \cap B)\), we get \[P(B) = P\big(A \cup (A^c \cap B)\big)\]
Since events \(A\) and \(A^c \cap B\) are disjoint, the probability of their union is just: \[P(A) + P(A^c \cap B)\]
Thus, our equation is now \[P(B) = P(A) + P(A^c \cap B)\]
From Axiom 1, we know for event \(A^c \cap B\), \(P(A^c \cap B) \geq 0\).
So the probability of event B is the sum of the probability of event A and an event that is \(\geq\) 0. This means \(P(B) \geq P(A)\).
Proposition 4
\(\mathbb{P}(A \cup B) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \cap B)\)
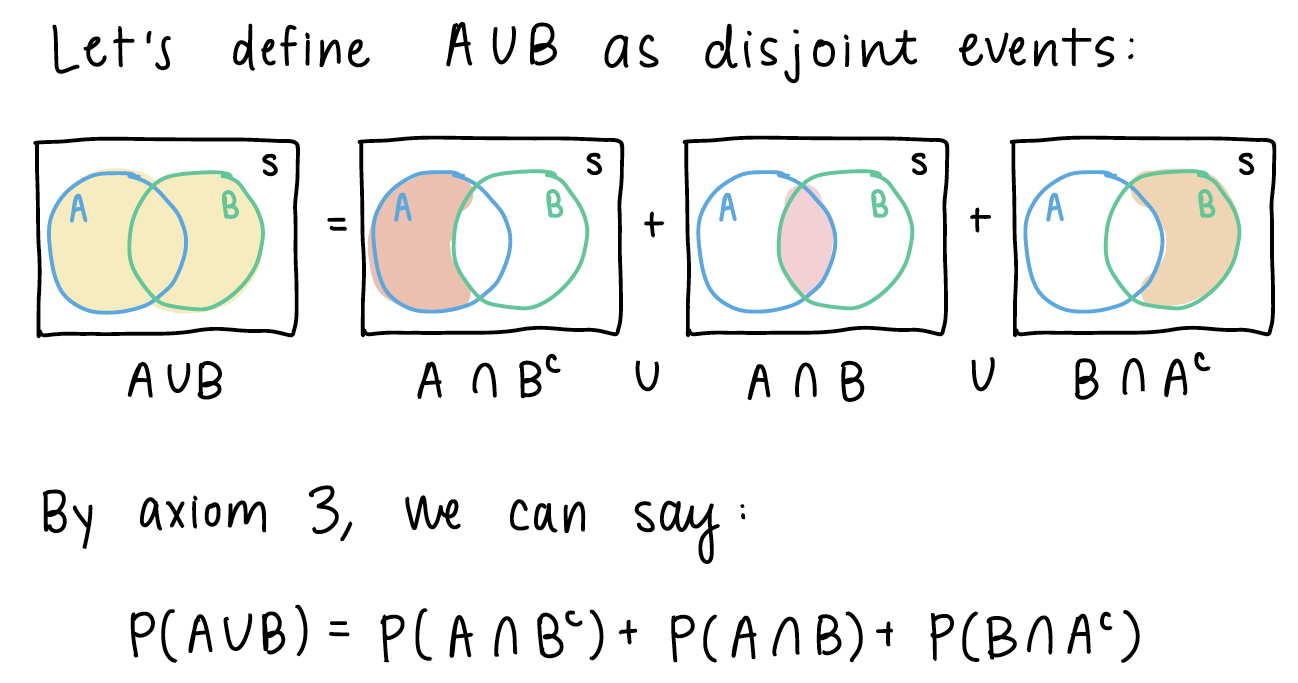
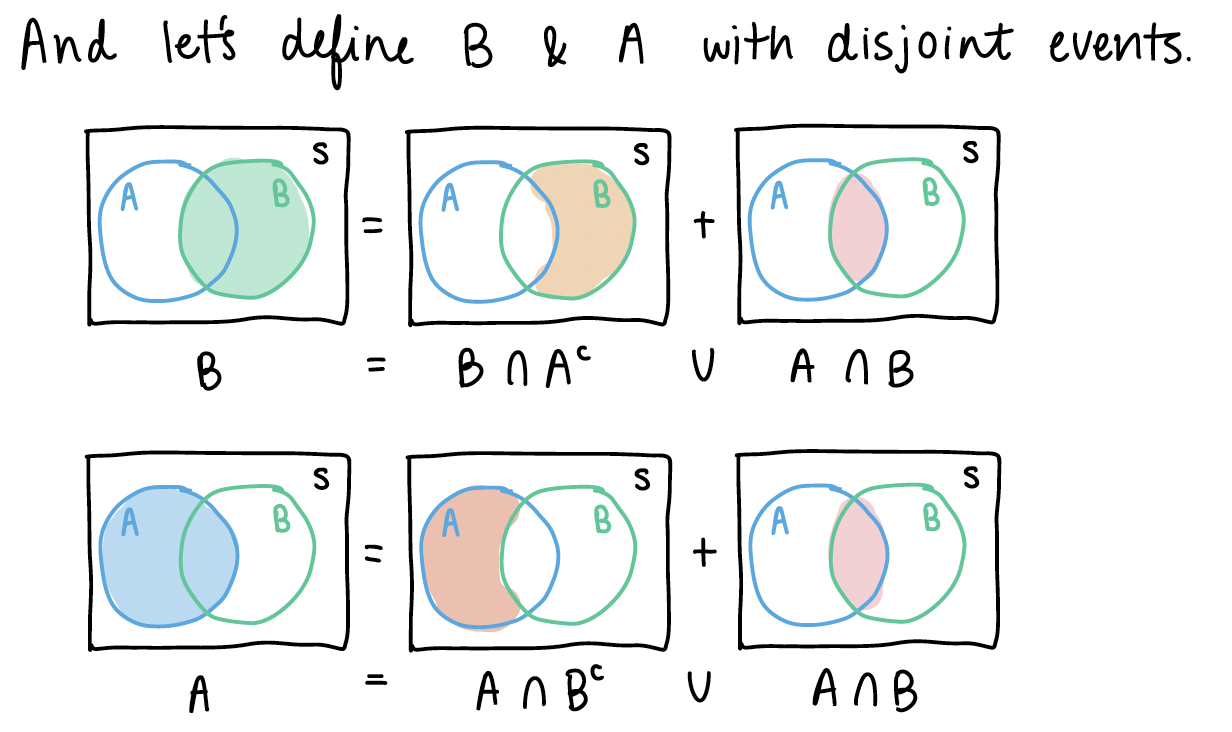
From the pictures above, we can see some similar disjoint events.
If we look back at \(A \cup B\), we can start manipulating the right side of the equation:
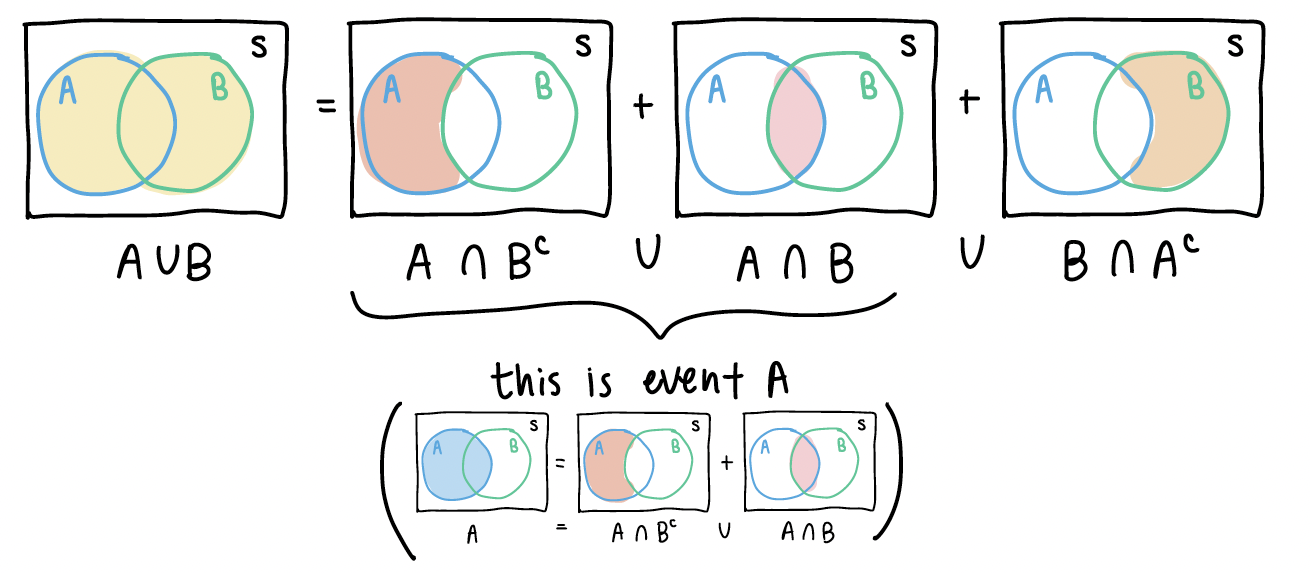
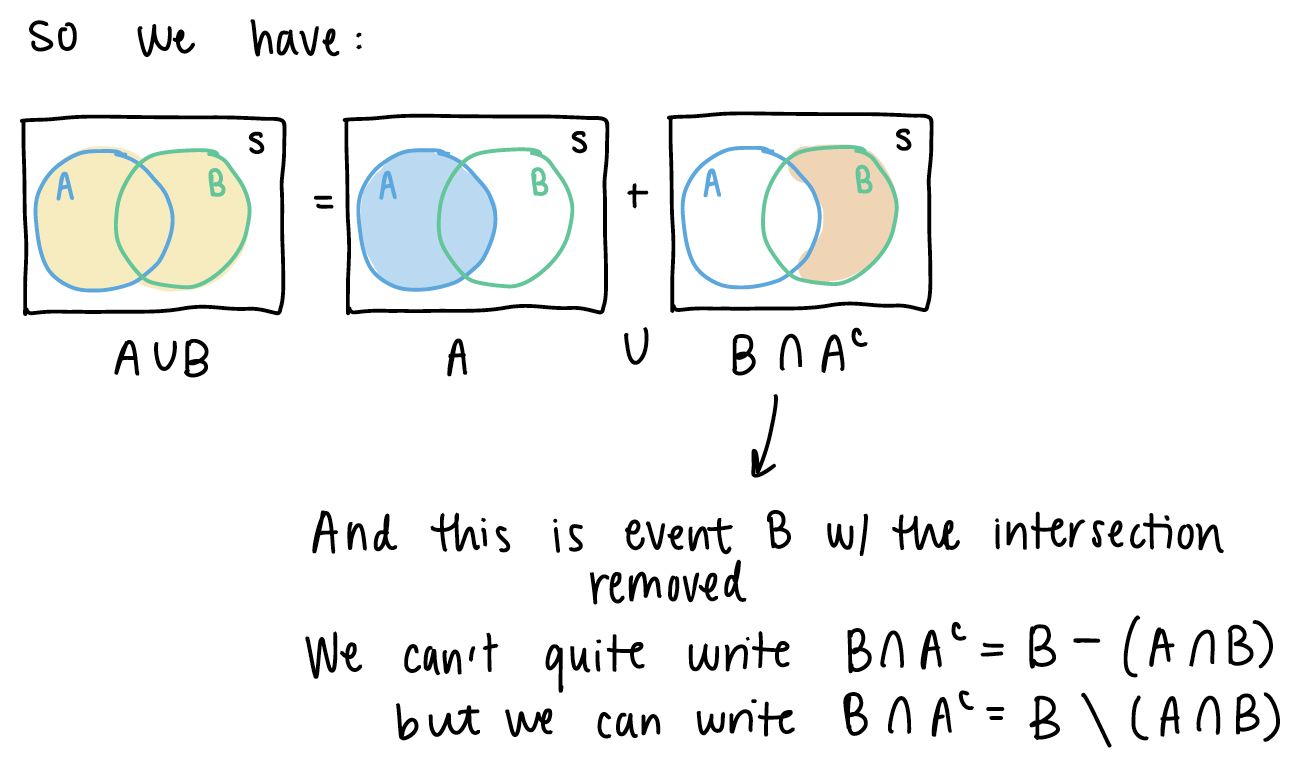
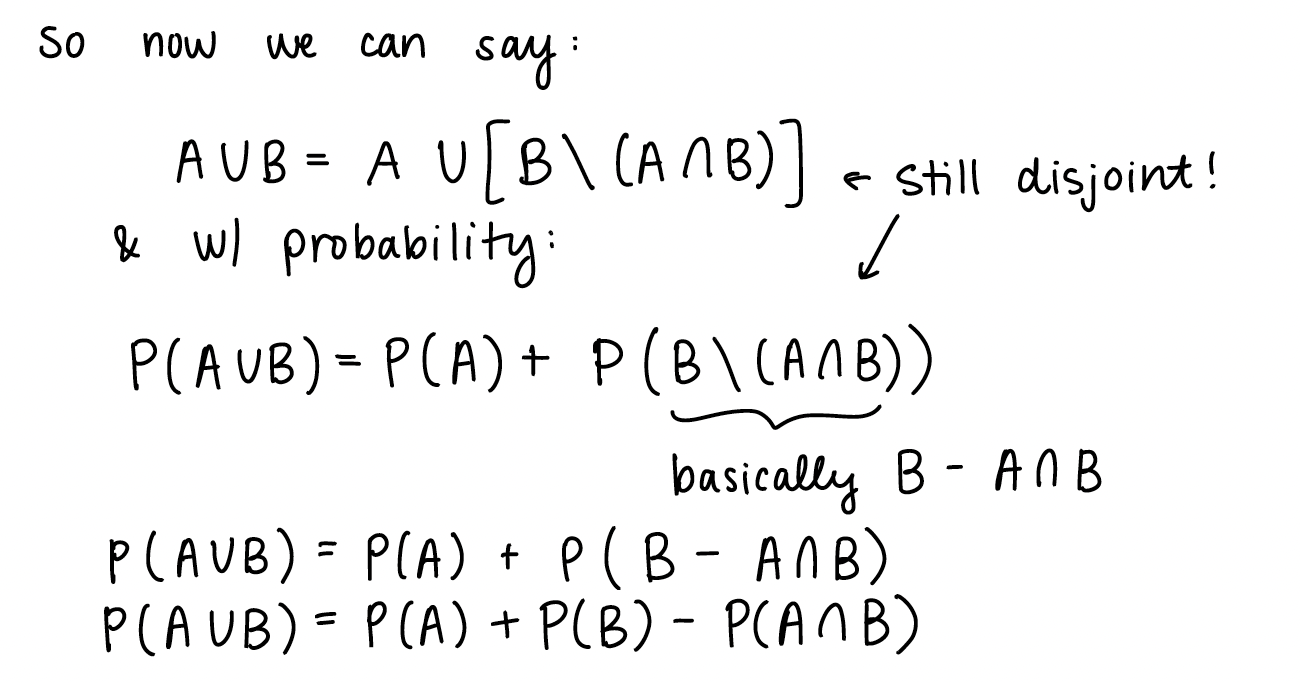
2. Example at end of Chapter 2 slides (Venn Diagram)
I will post this in the previous week’s Muddy Points as well. Please follow this link for my work through of the example. And here is the PDF with my work.
Sub-question: why don’t we just multiply the probability of A and B to get the intersection? This is a specific property of probability when A and B are independent. Only when A and B are independent can we conclude that \(P(A \cap B) = P(A)P(B)\).
3. Partition of events
We’ve been working with event partitions throughout Chapter 2, but we have not formally identified them. Partitions are advantageous to define for two reasons:
The partitions may be easier to calculate. We can then use the partitions to reconstruct other probabilities that may be more difficult to calculate
Partitions have nice properties as a consequence of being disjoint. For example, the probability of the union of partitions is the sum of the probabilities across each partition: \[P\bigg(\bigcup_{i=1}^n A_i\bigg) = P(A_1)P(A_2)P(A_3) \cdot \cdot \cdot P(A_n)\]