| Age Group | Hypertension | No Hypertension | Total |
|---|---|---|---|
| 18-39 years | 8836 | 112206 | 121042 |
| 40 to 59 years | 42109 | 88663 | 130772 |
| Greater than 60 years | 39917 | 21589 | 61506 |
| Total | 90862 | 222458 | 313320 |
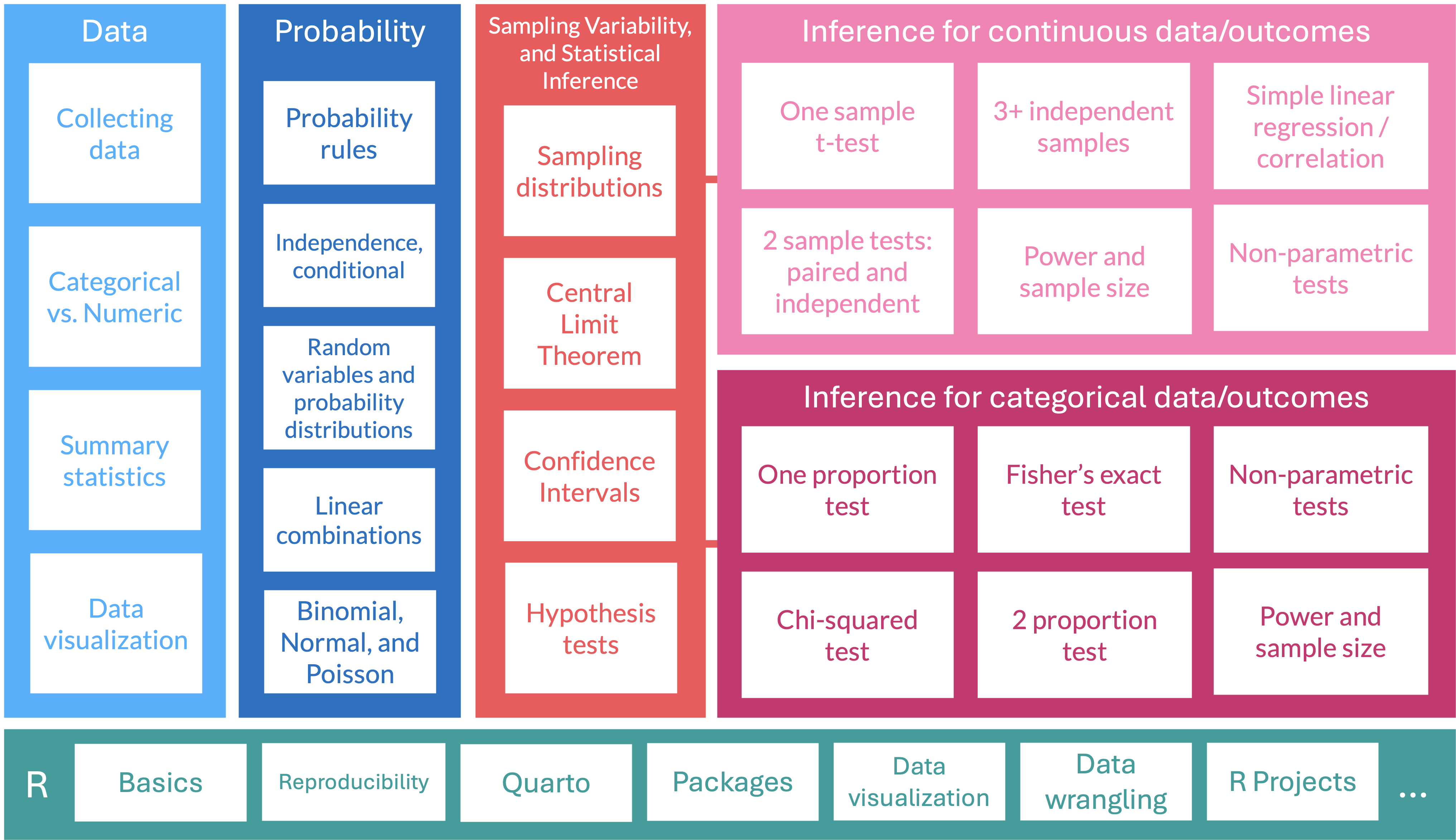
Lesson 4: Conditional Probability
TB sections 2.2
Learning Objectives
Recognize joint, marginal, and conditional probabilities in contingency and probability tables
Mathematically define probability properties that relate to conditional probability (general multiplication rule, independence and conditional probability, and Bayes’ theorem)
Apply probability properties to solve a world problem on positive predictive value (PPV)
Where are we?
Learning Objectives
- Recognize joint, marginal, and conditional probabilities in contingency and probability tables
Mathematically define probability properties that relate to conditional probability (general multiplication rule, independence and conditional probability, and Bayes’ theorem)
Apply probability properties to solve a world problem on positive predictive value (PPV)
Example: hypertension prevalence (1/2)
- US CDC estimated that between 2011 and 20141, 29% of the population in America had hypertension
- A health care practitioner seeing a new patient would expect a 29% chance that the patient might have hypertension
- However, this is only the case if nothing else is known about the patient
Example: hypertension prevalence (2/2)
- Prevalence of hypertension varies significantly with age
- Among adults aged 18-39, 7.3% have hypertension
- Adults aged 40-59, 32.2%
- Adults aged 60 or older, 64.9% have hypertension
Knowing the age of a patient provides important information about the likelihood of hypertension
- Age and hypertension status are not independent (we will get into this)
While the probability of hypertension of a randomly chosen adult is 0.29…
- The conditional probability of hypertension in a person known to be 60 or older is 0.649
How can we assemble the full picture of hypertension and age with probabilities?
Contingency tables
- We can start looking at the contingency table for hypertension for different age groups
- Contingency table: type of data table that displays the frequency distribution of two or more categorical variables
Types of probabilities from contingency tables
| Age Group | Hypertension | No Hypertension | Total |
|---|---|---|---|
| 18-39 years | 8836 | 112206 | 121042 |
| 40 to 59 years | 42109 | 88663 | 130772 |
| Greater than 60 years | 39917 | 21589 | 61506 |
| Total | 90862 | 222458 | 313320 |
Joint probability
- In first row, shows that in the entire population of 313,320,000, approximately 8,836,000 people were aged 18-39 years and had hypertension (~2.8%)
Marginal probability
- We can say that in the entire population of 313,320,000, approximately 121,042,000 people are 18-39 years (~38.6%)
Conditional probability
- But we can also say the first row shows that of 121,042,000 people who are 18-39 years, 8,836,000 people had hypertension (~7.3%)
Poll Everywhere Question 1
Probability tables
We typically display joint and marginal probabilities in probability table
| Age Group | Hypertension | No Hypertension | Total |
|---|---|---|---|
| 18-39 years | 0.0282 | 0.3581 | 0.3863 |
| 40 to 59 years | 0.1344 | 0.2830 | 0.4174 |
| Greater than 60 years | 0.1274 | 0.0689 | 0.1963 |
| Total | 0.2900 | 0.7100 | 1.0000 |
Joint probability: intersection of row and column
Marginal probability: row or column total
Let’s go back to conditional probability
- So far we have intuitively thought of conditional probability and used the contingency table:
- The first row shows that of 121,042,000 people who are 18-39 years, 8,836,000 people had hypertension (~7.3%)
- We got this from: \[P(\text{hypertension} | \text{18-39 years old}) = \dfrac{8,836,000}{121,042,000} = 0.073\]
- “\(\text{hypertension} | \text{18-39 years old}\)” reads as “hypertension given 18-39 years old”
Can we calculate the conditional probability from the probability table?
Learning Objectives
- Recognize joint, marginal, and conditional probabilities in contingency and probability tables
- Mathematically define probability properties that relate to conditional probability (general multiplication rule, independence and conditional probability, and Bayes’ theorem)
- Apply probability properties to solve a world problem on positive predictive value (PPV)
We can define conditional probability more mathematically
- Let’s define some events:
- \(A\) = hypertension
- \(B\) = 18-39 years old
\[P(\text{hypertension} | \text{18-39 years old}) = P(A | B) = \dfrac{P(A \cap B)}{P(B)}\]
Conditional probability
The conditional probability of an event A given an event or condition B is: \[P(A|B) = \frac{P(A \cap B)}{P(B)}\]
So if we had a table of probabilities for our example…
| Age Group | Hypertension | No Hypertension | Total |
|---|---|---|---|
| 18-39 years | 0.0282 | 0.3581 | 0.3863 |
| 40 to 59 years | 0.1344 | 0.2830 | 0.4174 |
| Greater than 60 years | 0.1274 | 0.0689 | 0.1963 |
| Total | 0.2900 | 0.7100 | 1.0000 |
What is the probability of hypertension for someone aged 18-39 years old?
Recall
- \(A\) = hypertension
- \(B\) = 18-39 years old
- \[P(A|B) = \frac{P(A \cap B)}{P(B)}\]
General multiplication rule
General multiplication rule
If \(A\) and \(B\) represent two outcomes or events, then \[P(A \cap B) = P(A|B)P(B)\]
This follows from rearranging the definition of conditional probability: \[P(A|B) = \frac{P(A \cap B)}{P(B)} \rightarrow P(A|B)P(B) = P(A \cap B)\]
Independence and conditional probability
If two events, say A and B, are independent, then: \[P(A \cap B) = P(A)P(B)\]
We can extend this to conditional probability: \(P(A|B) = \frac{P(A \cap B)}{P(B)}\)
- For two independent events, say A and B, \[P(A|B) = \frac{P(A \cap B)}{P(B)} = \frac{P(A)P(B)}{P(B)} = P(A)\]
Conditional probability of independent events
If events A and B are independent, then \[P(A|B) =P(A) \text{ and } P(B|A) = P(B)\]
Poll Everywhere Question 2
Bayes’ Theorem (Section 2.2.5)
Bayes’ Theorem
In its simplest form: \[P(A|B) = \frac{P(B|A)P(A)}{P(B)}\]
This also translates to: \[P(A | B) = \frac{P(B|A) \cdot P(A)} {P(B|A) \cdot P(A) + P(B|A^c) \cdot P(A^c) }\] because of the Law of Total Probability: \[\begin{aligned}P(B) = & P(B \cap A) + P(B \cap A^C) \\ = &P(B | A)P(A)+ P(B|A^C)P(A^C) \end{aligned}\]
Learning Objectives
Recognize joint, marginal, and conditional probabilities in contingency and probability tables
Mathematically define probability properties that relate to conditional probability (general multiplication rule, independence and conditional probability, and Bayes’ theorem)
- Apply probability properties to solve a world problem on positive predictive value (PPV)
Example: How accurate is rapid testing for COVID-19? (1/n)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Suppose you take the iHealth® rapid test.
What is the probability of a positive test result?
What is the probability of having COVID-19 if you get a positive test result?
What is the probability of not having COVID-19 if you get a negative test result?
From the iHealth® website https://ihealthlabs.com/pages/ihealth-covid-19-antigen-rapid-test-details:
Some specialized terminology in diagnostic tests
Calculating probabilities for diagnostic tests is done so often in medicine that the topic has some specialized terminology
- The sensitivity of a test is the probability of a positive test result when disease is present, such as a positive mammogram when a patient has breast cancer.
- The specificity of a test is the probability of a negative test result when disease is absent
- The probability of disease in a population is referred to as the prevalence.
- With specificity and sensitivity information for a particular test, along with disease prevalence, the positive predictive value (PPV) can be calculated: the probability that disease is present when a test result is positive.
- Similarly, the negative predictive value is the probability that disease is absent when test results are negative
Poll Everywhere Question 3
General steps for probability word problems
Define the events in the problem and draw a Venn Diagram
Translate the words and numbers into probability statements
Translate the question into a probability statement
Think about the various definitions and rules of probabilities. Is there a way to define our question’s probability statement (in step 3) using the probability statements with assigned values (in step 2)?
Plug in the given numbers to calculate the answer!
Let’s apply the steps to our example (1/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 1: Let’s define our events of interest
\(D\) = event one has disease (COVID-19)
\(D^c\) = event one does not have disease
\(T^+\) = event one tests positive for disease
\(T^-\) = event one tests negative for disease
Let’s apply the steps to our example (2/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 2: Translate given information into mathematical notation
- Test correctly gives a positive result 94.3% of the time:
- Test correctly gives a negative result 98.1% of the time:
- 83.8 people per 100k in Multnomah County with Covid-19:
Let’s apply the steps to our example (3/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 3: Translate the question into a probability statement
- What is the probability of a positive test result?
- What is the probability of having COVID-19 if you get a positive test result?
- What is the probability of not having COVID-19 if you get a negative test result?
Let’s apply the steps to our example (4/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 4: Define our question’s probability statement using the probability statements with assigned values
- \(P(T^{+}) =\)
Let’s apply the steps to our example (5/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 4: Define our question’s probability statement using the probability statements with assigned values
- \(P(D|T^{+}) =\)
Let’s apply the steps to our example (6/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 4: Define our question’s probability statement using the probability statements with assigned values
- \(P(D^{\text{c}}|T^{-}) =\)
Let’s apply the steps to our example (7/7)
How accurate is rapid testing for COVID-19?
“Based on the results of a clinical study where the iHealth® COVID-19 Antigen Rapid Test was compared to an FDA authorized molecular SARS-CoV-2 test, iHealth® COVID-19 Antigen Rapid Test correctly identified 94.3% of positive specimens and 98.1% of negative specimens.” In October 2022, 83.8 people per 100k in Multnomah County with Covid-19.
Step 5: Calculate answer